Естественный способ задания движения точки
 При естественном способе задания движения задаются траектория и закон движения точки по траектории. Движение точки рассматривается относительно фиксированной системы
При естественном способе задания движения задаются траектория и закон движения точки по траектории. Движение точки рассматривается относительно фиксированной системы 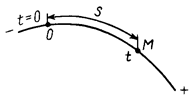 отсчета.
отсчета.
Для задания закона движения точки по траектории необходимо выбрать на траектории точку 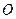 , принимаемую за начало отсчета расстояний (рис. 25). Расстояния в одну сторону от точки
, принимаемую за начало отсчета расстояний (рис. 25). Расстояния в одну сторону от точки 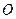 по траектории считаются положительными (например, вправо), в другую – отрицательными. Кроме того, следует задать начало отсчета времени. Обычно за
по траектории считаются положительными (например, вправо), в другую – отрицательными. Кроме того, следует задать начало отсчета времени. Обычно за 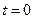 принимают момент времени, в который движущаяся точка проходит через точку
принимают момент времени, в который движущаяся точка проходит через точку 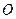 , или момент начала движения. Время до этого события считается отрицательным, а после него – положительным.
, или момент начала движения. Время до этого события считается отрицательным, а после него – положительным.
Если в момент времени 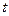 движущаяся точка занимает положение
движущаяся точка занимает положение 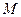 , то закон движения точки по траектории задается зависимостью от времени расстояния
, то закон движения точки по траектории задается зависимостью от времени расстояния 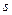 , отсчитываемого от точки
, отсчитываемого от точки 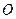 до точки
до точки 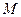 , т. е.
, т. е. 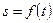 . Эта функция должна быть непрерывной и дважды дифференцируемой.
. Эта функция должна быть непрерывной и дважды дифференцируемой.
При естественном способе задания движения используется понятие естественных осей координат. Сначала в точке строится соприкасающаяся окружность, которая наиболее плотно смыкается с траекторией из всех возможных. Ее центр называют центром кривизны траектории. Плоскость, в которой лежит соприкасающаяся окружность, называется соприкасающейся плоскостью.
Построим в точке 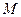 кривой линии естественные оси этой кривой (рис. 26). Первой естественной осью является касательная
кривой линии естественные оси этой кривой (рис. 26). Первой естественной осью является касательная 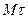 . Ее положительное направление совпадает с направлением единичного вектора касательной
. Ее положительное направление совпадает с направлением единичного вектора касательной 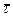 , направленного в сторону возрастающих расстояний.
, направленного в сторону возрастающих расстояний.

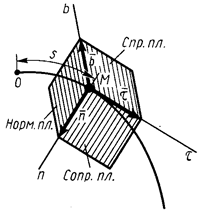 Перпендикулярно касательной
Перпендикулярно касательной 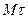 располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью
располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью 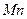 . Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью.
. Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью.
По главной нормали внутрь вогнутости кривой направим единичный вектор 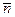 . Он определяет положительное направление второй естественной оси.
. Он определяет положительное направление второй естественной оси.
Нормаль, перпендикулярная главной нормали, называется бинормалью. Единичный вектор 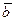 , направленный по бинормали так, чтобы три вектора
, направленный по бинормали так, чтобы три вектора 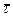 ,
, 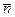 и
и 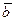 образовывали правую систему осей координат, определит положительное направление третьей естественной оси.
образовывали правую систему осей координат, определит положительное направление третьей естественной оси.
Три взаимно перпендикулярные оси 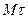 ,
, 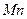 и
и 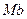 , положительные направления которых совпадают с направлениями единичных векторов
, положительные направления которых совпадают с направлениями единичных векторов 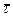 ,
, 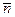 и
и 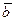 , называются естественными осями кривой. Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.
, называются естественными осями кривой. Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.
Используя определение скорости, имеем:
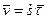 ,
,
где 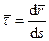 . Вектор
. Вектор 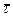 направлен по касательной к траектории как производная от вектора по скалярному аргументу и является единичным вектором. Модуль этого вектора равен единице, как предел отношения длины хорды
направлен по касательной к траектории как производная от вектора по скалярному аргументу и является единичным вектором. Модуль этого вектора равен единице, как предел отношения длины хорды 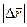 к длине стягивающей ее дуги
к длине стягивающей ее дуги 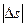 при стремлении ее к нулю.
при стремлении ее к нулю.
Единичный вектор 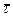 всегда направлен по касательной к траектории в сторону возрастающих (положительных) расстояний независимо от направления движения точки.
всегда направлен по касательной к траектории в сторону возрастающих (положительных) расстояний независимо от направления движения точки.
Величина 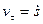 называется алгебраической скоростью точки. Ее можно считать проекцией скорости на положительное направление касательной к траектории, совпадающее с направлением единичного вектора
называется алгебраической скоростью точки. Ее можно считать проекцией скорости на положительное направление касательной к траектории, совпадающее с направлением единичного вектора 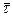 .
.
Естественное задание движения точки полностью определяет скорость точки по величине и направлению. Алгебраическую скорость находят дифференцированием по времени закона изменения расстояний. Единичный вектор 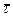 определяют по заданной траектории.
определяют по заданной траектории.
В соответствии с определением ускорения получаем
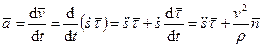 , (60)
, (60)
так как 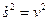 и
и 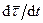 направлен внутрь вогнутости траектории параллельно единичному вектору главной нормали
направлен внутрь вогнутости траектории параллельно единичному вектору главной нормали 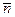 .
.
Получено разложение ускорения точки по осям естественного трехгранника. Касательная, нормальная составляющие и полное ускорение равны
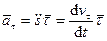 ,
, 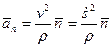 ,
, 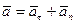 . (61)
. (61)
Дата добавления: 2017-01-29; просмотров: 899;
