Скорость и ускорение точки
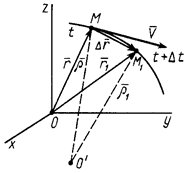 Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы координат (рис. 21).
Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы координат (рис. 21).
 Положение движущейся точки
Положение движущейся точки 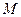 относительно рассматриваемой системы отсчета определяется в момент времени
относительно рассматриваемой системы отсчета определяется в момент времени  радиусом-вектором
радиусом-вектором  , который соединяет неподвижную точку
, который соединяет неподвижную точку 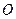 с этой точкой. В другой момент времени
с этой точкой. В другой момент времени 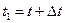 движущаяся точка займет положение
движущаяся точка займет положение 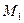 и ее радиусом-вектором будет
и ее радиусом-вектором будет 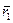 . За время
. За время 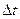 радиус-вектор движущейся точки изменится на
радиус-вектор движущейся точки изменится на  .
.
Средней скоростью 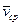 точки за время
точки за время 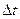 называют отношение
называют отношение  , т.е.:
, т.е.:
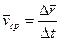 .
.
Средняя скорость параллельна вектору  . В общем случае она зависит от времени осреднения
. В общем случае она зависит от времени осреднения 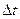 . У нее нет конкретной точки приложения на траектории.
. У нее нет конкретной точки приложения на траектории.
Введем скорость точки 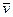 в момент
в момент  , которая определяется как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т. е.
, которая определяется как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т. е.
 .
.
Скорость точки направлена в сторону ее движения по предельному направлению вектора  при
при 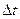 , стремящемся к нулю, т.е. по предельному направлению секущей
, стремящемся к нулю, т.е. по предельному направлению секущей  , которая совпадает с касательной к траектории в точке
, которая совпадает с касательной к траектории в точке 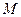 . Таким образом, скорость точки равна первой производной по времени от ее радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки.
. Таким образом, скорость точки равна первой производной по времени от ее радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки.
Начало радиуса-вектора движущейся точки можно выбрать в любой неподвижной точке. На рис. 21 представлен случай, в котором радиусом-вектором является также  с началом в точке
с началом в точке 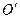 . Радиусы-векторы имеют одинаковые изменения
. Радиусы-векторы имеют одинаковые изменения  и
и 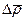 за время
за время 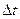 и поэтому
и поэтому
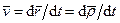 . (44)
. (44)
Пусть движущаяся точка 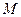 в момент времени
в момент времени  имеет скорость
имеет скорость 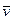 . В момент времени
. В момент времени 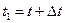 эта точка занимает положение
эта точка занимает положение 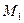 , имея скорость
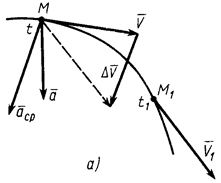
, имея скорость 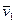 (рис. 22). Чтобы изобразить приращение скорости
(рис. 22). Чтобы изобразить приращение скорости  за время
за время 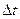 , перенесем вектор скорости
, перенесем вектор скорости 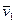 параллельно самому себе в точку
параллельно самому себе в точку 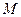 .
.

 Средним ускорением точки
Средним ускорением точки  за время
за время 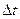 называют отношение
называют отношение  , т.е.
, т.е.  . Среднее ускорение точки параллельно приращению скорости
. Среднее ускорение точки параллельно приращению скорости  . Как и средняя скорость, среднее ускорение не имеет на траектории конкретной
. Как и средняя скорость, среднее ускорение не имеет на траектории конкретной  течки приложения и изображено в точке
течки приложения и изображено в точке 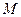 условно. В общем случае среднее ускорение зависит от времени
условно. В общем случае среднее ускорение зависит от времени 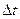 .
.
Ускорением точки  в момент времени
в момент времени  называют предел, к которому стремится среднее ускорение при
называют предел, к которому стремится среднее ускорение при 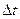 , стремящемся к нулю, т. е.
, стремящемся к нулю, т. е.
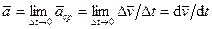 . (45)
. (45)
Таким образом, ускорение точки равно первой производной по времени от скорости точки.
Приращение скорости  и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при
и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при 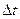 , стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории.
, стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории.
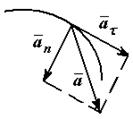 Ускорение точки можно представить в виде (рис. 23):
Ускорение точки можно представить в виде (рис. 23):
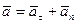 . (46)
. (46)
Часть ускорения, равная

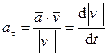 ,
,
называется касательной составляющей ускорения. Она направлена по касательной к траектории. Другая часть ускорения
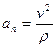
называется нормальной составляющей ускорения (  – радиус кривизны траектории). Она направлена внутрь вогнутости траектории, перпендикулярно
– радиус кривизны траектории). Она направлена внутрь вогнутости траектории, перпендикулярно  .
.
 2.1.2. Векторный способ задания движения точки
2.1.2. Векторный способ задания движения точки
 Движение точки относительно рассматриваемой системы отсчета при векторном способе изучения движения задается радиусом-вектором
Движение точки относительно рассматриваемой системы отсчета при векторном способе изучения движения задается радиусом-вектором  этой точки (рис. 24). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т. е.
этой точки (рис. 24). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т. е.
 . (47)
. (47)
Задание векторного уравнения движения (47) полностью определяет движение точки.
Скорость точки направлена по касательной к траектории и вычисляется, согласно ее определению, по формуле:
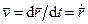 . (48)
. (48)
Для ускорения точки соответственно имеем
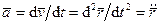 . (49)
. (49)
Определение скорости и ускорения точки сводится к чисто математической задаче вычисления первой и второй производных по времени от радиуса-вектора этой точки.
Дата добавления: 2017-01-29; просмотров: 653;
