Амплитуда и скорость распространения волн давления
В трубопроводе
Параметры волн давления в трубопроводе определяются основными законами механики – законом сохранения массы жидкости и законом изменения количества движения. Применим эти законы к возмущенному участку трубопровода.
Пусть за время 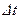 возмущение (для определенности, торможение) охватило область
возмущение (для определенности, торможение) охватило область 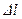 трубопровода (рис. 12.3).
трубопровода (рис. 12.3).
Баланс массы. Изменение 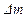 массы жидкости на участке
массы жидкости на участке 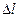 трубопровода равно, с одной стороны:
трубопровода равно, с одной стороны:
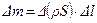
или
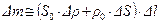 ,
,
с другой стороны, оно равно массе жидкости 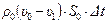 , вошедшей за время
, вошедшей за время 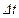 на рассматриваемый участок. Здесь
на рассматриваемый участок. Здесь 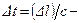 интервал времени, за который волна возмущения распространилась на расстояние
интервал времени, за который волна возмущения распространилась на расстояние 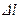 . Таким образом, баланс массы имеет вид:
. Таким образом, баланс массы имеет вид:
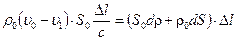 .
.
Разделив обе части этого уравнения на 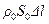 , получим:
, получим:
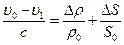 . (12.5)
. (12.5)
Подставив в эту формулы выражения (12.3) и (12.4) для относительных изменений 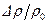 плотности жидкости и
плотности жидкости и 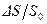 площади сечения трубопровода, получим равенство:
площади сечения трубопровода, получим равенство:
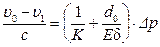 , (12.6)
, (12.6)
позволяющее установить связь изменения 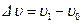 скорости течения жидкости в трубопроводе с изменением
скорости течения жидкости в трубопроводе с изменением 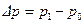 давления.
давления.
Баланс количества движения. При изменении скорости течения жидкости происходит изменение количества движения: при торможении – уменьшение, при ускорении - увеличение. Согласно второму закону Ньютона, эти изменения вызываются действием импульса 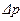 сил давления: при торможении потока давление возрастает (
сил давления: при торможении потока давление возрастает ( 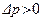 ), при ускорении – убывает (
), при ускорении – убывает ( 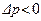 ).
).
Вычислим изменение 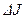 количества движения. Имеем:
количества движения. Имеем:
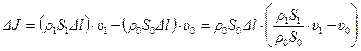 .
.
Поскольку
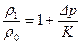 и
и 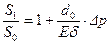 ,
,
то
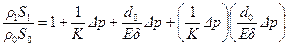 .
.
Три последние члена в правой части полученной формулы малы по сравнению с 1, поэтому ими можно пренебречь, т.е. считать, что 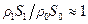 . Поэтому с точностью до малых более высокого порядка, имеем
. Поэтому с точностью до малых более высокого порядка, имеем
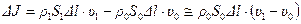 .
.
Согласно второму закону Ньютона, изменение 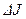 количества движения системы материальных точек равно импульсу всех внешних сил, действующих на эту систему, т.е.
количества движения системы материальных точек равно импульсу всех внешних сил, действующих на эту систему, т.е.
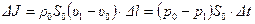 .
.
Учитывая, что 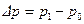 и
и 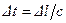 , получаем формулу:
, получаем формулу:
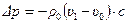 ,
,
связывающую изменение давления 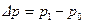 в трубопроводе, вызываемое изменением
в трубопроводе, вызываемое изменением 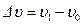 скорости течения жидкости, причем из этой формулы видно, что замедление потока
скорости течения жидкости, причем из этой формулы видно, что замедление потока 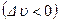 вызывает повышение давления, а ускорение потока
вызывает повышение давления, а ускорение потока 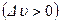 - понижение давления. Очевидно, эта формула обобщает ранее полученную формулу (12.1).
- понижение давления. Очевидно, эта формула обобщает ранее полученную формулу (12.1).
Если принять, что скорость 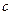 распространения волны возмущения может быть как положительной (когда волна распространяется вниз по потоку) и отрицательной (когда волна распространяется вверх по потоку), как в данном случае, то полученную формулу можно записать в универсальном виде:
распространения волны возмущения может быть как положительной (когда волна распространяется вниз по потоку) и отрицательной (когда волна распространяется вверх по потоку), как в данном случае, то полученную формулу можно записать в универсальном виде:
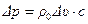 . (12.7)
. (12.7)
Формула (12.7)представляет собой первую формулу Н.Е.Жуковского. Формула Жуковского гласит: изменение скорости течения жидкости в трубопроводе вызывает пропорциональное ему изменение давления и наоборот, изменение давления в потоке жидкости, текущей в трубопроводе, приводит к пропорциональному изменению скорости течения.
Подставив (12.7) в (12.6)
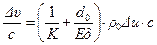
и сократив на 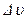 , получим вторую формулу Н.Е.Жуковского:
, получим вторую формулу Н.Е.Жуковского:
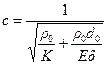 . (12.8)
. (12.8)
Эта формула устанавливает связь скорости распространения волн давления в трубопроводе с параметрами жидкости и самого трубопровода.
Пример 1. Вычислить скорость 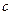 распространения волн давления при перекачке нефти
распространения волн давления при перекачке нефти 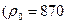 кг/м3,
кг/м3, 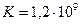 Па) по нефтепроводу
Па) по нефтепроводу 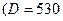 мм,
мм, 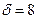 мм,
мм, 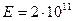 Па).
Па).
Решение. По формуле (12.8) находим:
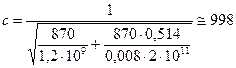 м/с.
м/с.
Пример 2. Рассчитать изменение 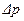 давления при изменении скорости течения нефти
давления при изменении скорости течения нефти 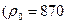 кг/м3,
кг/м3, 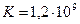 Па) на 1 м/с в трубопроводе (
Па) на 1 м/с в трубопроводе ( 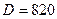 мм,
мм, 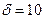 мм,
мм, 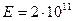 Па)
Па)
Решение. По формуле (12.8) находим:
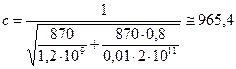 м/с.
м/с.
По формуле (12.7) рассчитываем 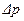 :
:
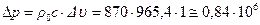 Па или
Па или 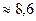 атм.
атм.
Пример 3. Рассчитать ударное изменение 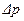 давления при внезапном закрытии задвижки в потоке нефти
давления при внезапном закрытии задвижки в потоке нефти 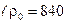 кг/м3,
кг/м3, 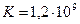 Па) транспортируемой с расходом 4200 м3/ч в трубопроводе (
Па) транспортируемой с расходом 4200 м3/ч в трубопроводе ( 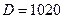 мм,
мм, 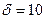 мм,
мм, 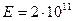 Па)
Па)
Решение. Сначала находим скорость 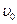 течения нефти:
течения нефти:
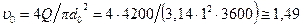 м/с.
м/с.
Затем по формуле (12.8) находим скорость волн давления:
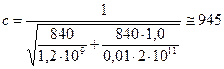 м/с.
м/с.
Наконец, по формуле (12.7) рассчитываем 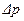 :
:
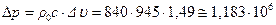 Па
Па 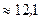 атм.
атм.
Пример 4. Оператор насосной станции совершил ошибку, включив станцию на закрытую задвижку. В результате нефть 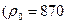 кг/м3,
кг/м3, 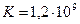 Па) стала подаваться в трубопровод (
Па) стала подаваться в трубопровод ( 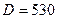 мм,
мм, 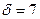 мм,
мм, 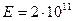 Па) с расходом 1300 м3/ч. Рассчитать ударное повышение
Па) с расходом 1300 м3/ч. Рассчитать ударное повышение 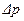 давления.
давления.
Решение. Сначала находим скорость 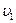 закачки нефти в трубопровод:
закачки нефти в трубопровод:
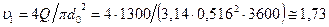 м/с.
м/с.
По формуле (12.8) находим скорость волн давления:
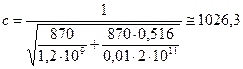 м/с.
м/с.
По формуле (12.7) рассчитываем 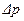 :
:
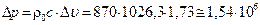 Па (
Па ( 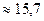 атм.)
атм.)
Пример 5. На сколько атмосфер понизится давление за мгновенно закрывшейся задвижкой, перекрывшей поток нефти 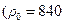 кг/м3,
кг/м3, 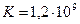 Па) транспортируемой с расходом 1300 м3/ч в трубопроводе (
Па) транспортируемой с расходом 1300 м3/ч в трубопроводе ( 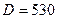 мм,
мм, 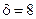 мм,
мм, 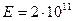 Па)
Па)
Решение. Находим скорость 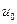 течения нефти:
течения нефти:
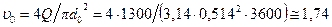 м/с.
м/с.
По формуле (12.8) находим скорость волн давления:
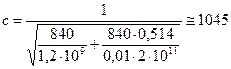 м/с.
м/с.
По формуле (12.7) рассчитываем 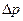 :
:
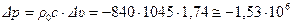 Па
Па 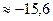 атм.
атм.
Если давление в месте установки задвижки было ниже 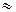 15 атм., то нефть за задвижкой может вскипеть, поскольку давление в ней снизится до упругости насыщенных паров. В этом случае за задвижкой образуется парогазовая полость.
15 атм., то нефть за задвижкой может вскипеть, поскольку давление в ней снизится до упругости насыщенных паров. В этом случае за задвижкой образуется парогазовая полость.
Дата добавления: 2016-05-16; просмотров: 1853;
