Упрощающие допущения

При рассмотрении нестационарных течений многих капельных жидкостей (например, нефтей, нефтепродуктов, воды и т.п.), обычно принимаются следующие допущения и делаются следующие упрощения.

· нефть считается слабо сжимаемой жидкостью, т.е. в уравнении состояния 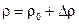считается, что 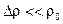, поэтому во всех коэффициентах плотность нефти заменяется ее невозмущенным значением;

· считается, что площадь сечения стального нефтепровода изменяется под воздействием давления крайне незначительно, т.е. 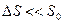, поэтому во всех коэффициентах площадь сечения трубопровода заменяется ее невозмущенным значением;

· изменениями величины скоростного напора пренебрегают по сравнению с изменениями пьезометрического напора: ;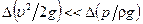

· принимается, что скорость 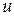течения жидкости в трубопроводе много меньше скорости 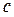распространения волн давления;

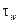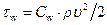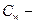· принимается так называемая гипотеза квазистационарности трения, согласно которой , представленное формулой , где коэффициент трения (или множитель Фанинга), выражается через коэффициент 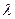гидравлического сопротивления:

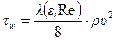(т.е. ),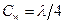

причем для коэффициента 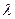используются зависимости, справедливые для стационарного течения.

Основные уравнения

С учетом сделанных допущений уравнение (12.8) преобразуется к виду:

.

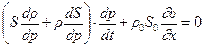Учитывая формулы (12.2), (12.4), согласно которым

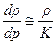и ,

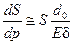получаем уравнение

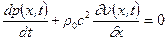, где .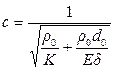

Можно показать, что из условия 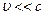следует, что 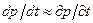. Тогда уравнение неразрывности получает окончательную форму:

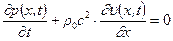. (12.12)

Уравнение (12.11) также упрощается и принимает вид:

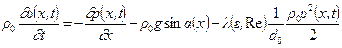. (12.13)

Таким образом, мы приходим к основной системе двух дифференциальных уравнений (12.12) и (12.13) с частными производными, используемых для расчета двух неизвестных функци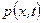й и .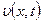

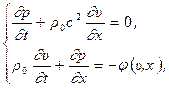(12.14)

где .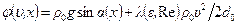

Если учесть, что 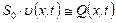; 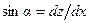и 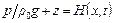, то систему уравнений, определяющих нестационарное течение нефти в трубопроводе, можно записать в терминах объемного расхода 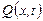и напора :

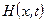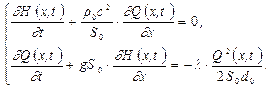(12.15)