Рекурсивные функции

Функция называется рекурсивной, если во время ее обработки возникает ее повторный вызов, либо непосредственно, либо косвенно, путем цепочки вызовов других функций.

Прямой (непосредственной) рекурсией является вызов функции внутри тела этой функции.

int a()

{.....a().....}

Косвенной рекурсией является рекурсия, осуществляющая рекурсивный вызов функции посредством цепочки вызова других функций. Все функции, входящие в цепочку, тоже считаются рекурсивными.

Например:

a(){.....b().....}

b(){.....c().....}

c(){.....a().....} .

Все функции a,b,c являются рекурсивными, так как при вызове одной из них, осуществляется вызов других и самой себя.

. Если функция вызывает себя, в стеке создается копия значений ее параметров, как и при вызове обычной функции, после чего управление передается первому исполняемому оператору функции. При повторном вызове этот процесс повторяется. Ясно, что для завершения вычислений каждая рекурсивная функция должна содержать хотя бы одну нерекурсивную ветвь алгоритма, заканчивающуюся оператором возврата. При завершении функции соответствующая часть стека освобождается, и управление передается вызывающей функции, выполнение которой продолжается с точки, следующей за рекурсивным вызовом.

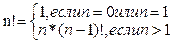
Числа Фибоначи f0=1

f1=1

fk=fk-1+fk-2

Простым примером рекурсии является функция factr(), вычисляющая факториал целого числа. Факториал числа N есть произведение целых чисел от 1 до N. Для вычисления факториала следует число п умножить на факториал числа п-1.Известно также что 0!=1 и 1!=1

/* Вычисление факториала числа */

int fact(int n) /* нерекурсивно */

{ int t, answer;

answer = 1;

for(t=1; t<=n; t++)

answer = answer*t;

return answer;

}

/* Вычисление факториала числа */

long factr(int n) /* рекурсивно */

{

if(n==1 || n==0)) return 1;

return fact(n-1)*n;

}

long factr(int n) /* рекурсивно */

{

return (n>1)?fact(n-1)*n:1;

}

При написании рекурсивных функций следует использовать оператор if, чтобы заставить функцию вернуться без рекурсивного вызова. Если это не сделать, то, однажды вызвав функцию, выйти из нее будет невозможно.

Достоинством рекурсии является компактная запись, а недостатками — расход времени и памяти на повторные вызовы функции и передачу ей копий параметров, и, главное, опасность переполнения стека.

Прімер. Программа упорядочивания по возрастания чисел методом быстрой сортировки, предложенной Хоар в 1961 г

Метод быстрой сортировки состоит в следующем:

Средний(один из средних) элемент принимается за эталонный и элементы последовательности меньшие эталонного перемещаются в левую часть, а большие – в правую. затем процесс повторяется для каждой из этих частей и будет завершен, когда в рассматриваемых частях останется по одному элементу. Данный метод сортировки является рекурсивным и самым эффективным

Метод быстрой сортировки. В массиве выбирается элемент относительно которого ведётся сортировка, как правило это средний элемент a[k]. Сначала перебираются все элементы расположенные слева от a[k], начиная с первого, до элемента большего либо равного по значению a[i]>=a[k]. После этого перебираются все элементы расположенные справа от a[k], начиная с последнего, до элемента меньшего либо равного по значению a[j]<=a[k]. Элементы a[i] и a[j] меняются местами. Эта процедура продолжается до тех пор, пока выполняется условие i<j. Если же это условие не выполняется то массив разбивается на два новых массива и все действия повторяются до тех пор, пока новый массив содержит не менее двух элементов.

#include<iostream.h>

#include<conio.h>

#include<stdlib.h>

void quicksort(int *a,int l,int r);

int main ()

{const int n=10;

int a[n],i;

randomize();

for(i=0;i<n;i++)

{a[i]=random(50);

cout<<a[i]<<" ";

}

quicksort(a,0,n-1);

cout<<"\nPosle\n";

for(i=0;i<n;i++)

cout<<a[i]<<" ";

getche();

}

void quicksort(int *a,int l,int r)

{

int i,j;

int buf,p;

if(l<r)

{p=a[(l+r)/2];

i=l;

j=r;

do

{while(a[i]<p) i++;

while(a[j]>p) j--;

if(i<=j)

{buf=a[i];

a[i]=a[j];

a[j]=buf;

i++;

j--;

}

} while(i<j);

quicksort(a,l,j);

quicksort(a,i,r);

}

}