Напруження в матеріалі проводу. Рівняння проводу.

Провід в прогоні повітряної лінії розглядаємо як ідеальну гнучку нитку підвішену у двох точках А і В (рис. 5.2). При цьому нехтуємо жорсткістю провода, вважаємо, що він не розтягується та має ідеальну гнучкість, а вага провода рівномірно розподілена по його довжині. На провід у будь-якій точці з координатами (х,у) діє сила натягу , яка направлена по дотичній до кривої провисання провода та приводить до виникнення в ньому напруження.

Рис. 5.2.

Сила натягу провода врівноважується вагою вертикального відрізку гнучкої нитки , яка звисає до осі абсцис через ідеальний блок (рис. 5.3), яка не співпадає з землею.

,

(5.9)

де g - питоме навантаження на провід.

Силу натягу провода в нижній точці 0 можна визначити за формулою

,

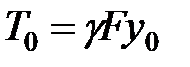(5.10)

а у точці підвісу проводу А за формулою

,

(5.11)

де f – стріла провисання проводу.

Напруження в матеріалі провода рівне силі натягу на одиницю перерізу. Відповідно у точках 0 і А (рис. 5.2) напруження визначають за формулами:

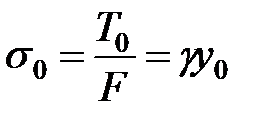;	(5.12)
.	(5.13)

У місцях підвісу напруження в проводі більше, ніж у його нижній точці, тобто .

На повітряних лініях, які проходять по непересічній місцевості та мають прогони нормальної довжини, різниця між і є дуже мала, не перевищує 0,3% і розраховують .

Рис. 5.3.

Рівняння кривої провисання проводу в прогоні має вигляд

,

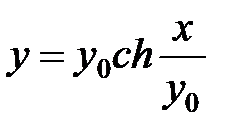(5.14)

де x,y – координати точки провода; - відстань від нижньої точки провисання провода до осі x.

Відстань від точки 0 до точки підвісу проводу А дорівнює половині довжини прогону l (рис. 5.2). Враховуючи це, рівняння (5.14) для точки підвісу проводу А набуває вигляду

.

(5.15)

Стрілу провисання проводу у точці 0 можна визначити за формулою

,

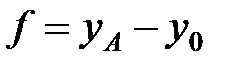(5.16)

або з врахуванням рівняння (12.14) – за формулою

.

(5.17)

Відстань від нижньої точки провисання провода до осі x, враховуючи, що , запишемо як 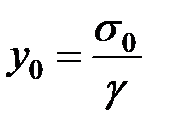. Тоді рівняння стріли провисання проводу в прогоні набуває вигляду

.

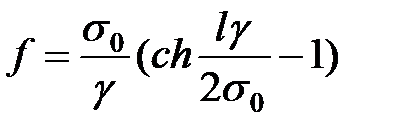(5.18)

Гіперболічний косинус розкладемо в ряд 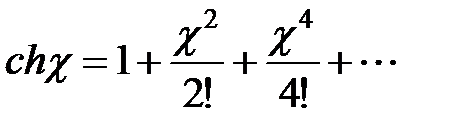та враховуючи, що , рівняння (5.18) запишемо у вигляді

.

(5.19)

Для прогонів повітряних ліній довжиною до 500 м стрілу провисання проводу можна визначати, враховуючи тільки перший член рівняння (5.19), за формулою

,

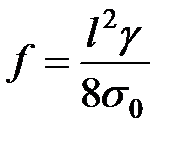(5.20)

де l - довжина прогону; g - питоме навантаження на провід за заданих кліматичних умов; - напруження в нижній точці провисання проводу в прогоні, яке відповідає питомому навантаженню g та заданих кліматичних умовах.

У випадку великих прогонів повітряних ліній, наприклад, переходу через широкі водойми, стрілу провисання проводу можна визначати, враховуючи перші два члени рівняння (5.19), за виразом

.

(5.21)

Під час практичних розрахунків замість рівняння ланцюгової лінії (5.14) та витікаючих з нього рівнянь (5.17) і (5.23) використовують більш прості рівняння параболи .

Довжину проводу в прогоні повітряної лінії від точки 0 (рис. 5.2) до точки з координатами (х,у) визначають за формулою

.

(5.22)

За умови, що (рис 5.2), довжину проводу в прогоні можна визначити за формулою

.

(5.23)

Гіперболічний синус розкладемо в ряд і рівняння (5.23) запишемо у вигляді

(5.24)

В прогонах повітряних ліній довжиною до 500 м довжину проводу можна визначати наближено за виразом

.

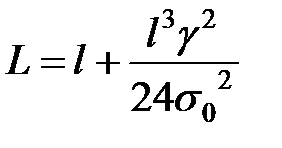(5.25)

Якщо довжина прогону перевищує 500 м, то для визначення довжини проводу необхідно використовувати рівняння

.

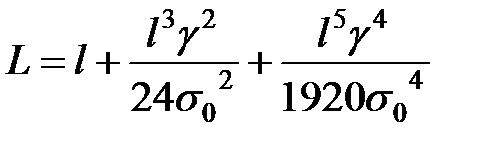(5.26)

Вираз (5.25) як і вираз (5.26) є рівнянням дуги параболи, використання якого для визначення стріли провисання проводу в прогоні та довжини проводу в прогоні повітряної лінії пов’язане з допущенням суть якого полягає у тому, що питоме навантаження g рівномірно розподілене по довжині прогону, а не по довжині проводу. За такого допущення довжина проводу в прогоні повітряної лінії відрізняється від довжини прогону менше, ніж 0,1%.