Дискретно-аналитический метод решения задачи.

Ниже рассмотрим дискретно-аналитический метод решения задачи, который состоит в следующем: по оси x осуществляется конечно-разностная аппроксимация, а по времени t рассматривается непрерывная (континуальная) задача.

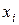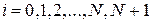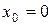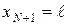Пусть , – координаты точек разбиения, причем и – граничные точки (в которых заданы краевые условия). Таким образом, искомыми будут являться функции 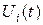, 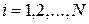во внутренних узлах сетки. Схема аппроксимации пространственно-временной области в данном случае условно показана на рис. 1.

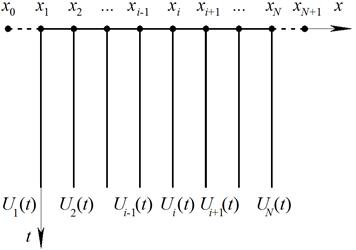
Рис. 1. Пространственно-временная область:

Во всех внутренних точках узлах 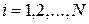уравнение теплопроводности в ( 37) примет вид:

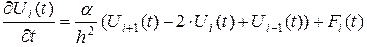( 40)

при этом пусть

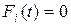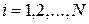, . ( 41)

В соответствии с краевыми условиями из ( 37) для граничных точек, в свою очередь, можем записать:

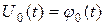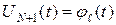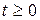, , . ( 42)

Следовательно, уравнения теплопроводности для узлов с номерам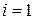и и 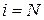имеют соответственно вид:

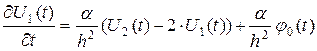; ( 43)

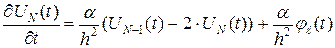. ( 44)

Введем обозначения:

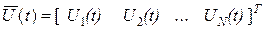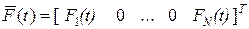; , ( 45)

где

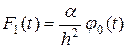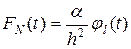; . ( 46)

Получаем матричную формулировку разрешающей системы уравнений:

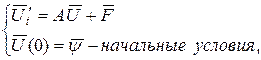( 47)

где

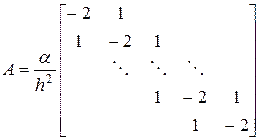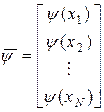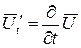; ; . ( 48)

Согласно ( 31)-( 32) общее решение задачи ( 47) имеет вид:

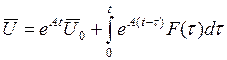. ( 49)

Если 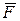не зависит от 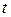, переходим к формуле

.

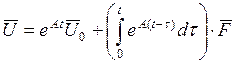Выполняем интегрирование:

,

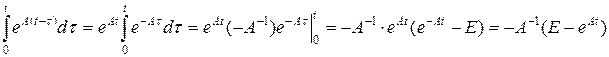откуда

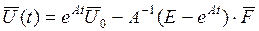. ( 50)

Реализация формулы ( 50) предполагает вычисление экспоненты от матрицы 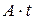, для выполнения которого следует воспользоваться результатами предыдущего параграфа (см. формулу ( 17)). Имеем:

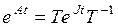, ( 51)

где

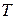– матрица собственных векторов матрицы ;

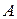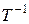– обратная матрица к матрице ;

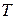; ( 52)

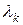– собственные числа матрицы , .

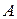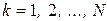Аналогично можем вычислить

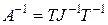, где 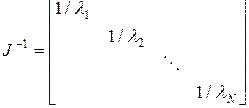. ( 53)

Варианты задания.

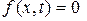– функция, характеризующая мощность источника тепла;

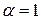– коэффициент температуропроводности материала стены;

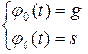– краевые условия;

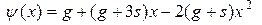– начальные условия;

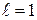– толщина стены; 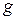– номер группы, 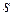– номер студента по журналу.

Текст М-файла

function teplo_1_expm

function U=ut(t)

E=eye(n);

eAt=expm(t*A);

U=eAt*U0-A\(E-eAt)*F;

end

s=input('s=');

g=input('g=');

n=input('n=');

L=input('L=');

alpha=input('alpha=');

h=L/(n+1);

c=alpha/h^2;

a1=ones(n-1,1);

A=diag(a1,-1)-2*eye(n)+diag(a1,1),A=c*A;

u0=g; ul=s;

F=c*[u0;zeros(n-2,1);ul];

xi=(0:h:L)';x=xi(2:n+1);

U0=g+(g+3*s)*x-2*(g+s)*x.^2;

t=[0 0.15 1.5];

nt=length(t);res=zeros(nt,n+2);

fprintf('\n значения функции температуры U(x,t)\n')

for i=1:nt

res(i,:)=[u0 ut(t(i))' ul];

fprintf('U(%4.2f):',t(i)),fprintf('%6.2f',res(i,:)),fprintf('\n')

end

hold on

plot(xi,res(1,:),'.-')

plot(xi,res(2,:),'o-.r')

plot(xi,res(nt,:),'*:g')

grid on

s1=sprintf('t=%2.0f',t(1));

s2=sprintf('t=%4.2f',t(2));

s3=sprintf('t=%4.2f',t(nt));

legend(s1,s2,s3,0)

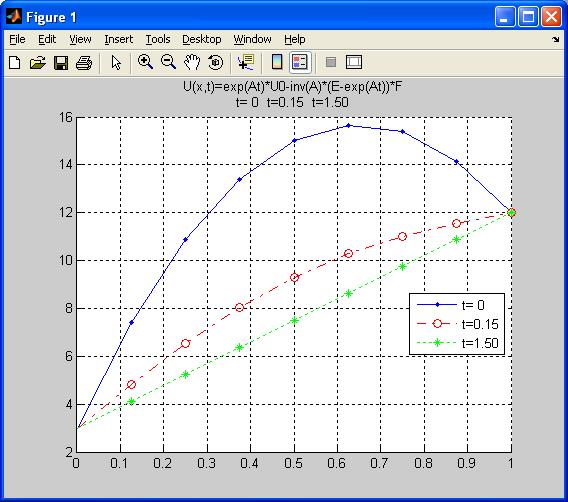
title(sprintf('U(x,t)=exp(At)*U0-inv(A)*(E-exp(At))*F\n%s %s %s', s1,s2,s3))

end

Результаты счета

s=12

g=3

n=7

L=1

alpha=1

A =

-2 1 0 0 0 0 0

1 -2 1 0 0 0 0

0 1 -2 1 0 0 0

0 0 1 -2 1 0 0

0 0 0 1 -2 1 0

0 0 0 0 1 -2 1

0 0 0 0 0 1 -2

значения функции температуры U(x,t)

U(0.00): 3.00 7.41 10.88 13.41 15.00 15.66 15.38 14.16 12.00

U(0.15): 3.00 4.81 6.52 8.03 9.29 10.28 11.02 11.56 12.00

U(1.50): 3.00 4.13 5.25 6.38 7.50 8.63 9.75 10.88 12.00

>>