Некоторые важные примеры приложений.
Пример 1. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка вида
 ( 31)
( 31)
где
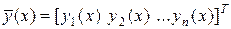 ;
;  , ( 32)
, ( 32)
причем 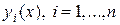 – искомые функции;
– искомые функции; 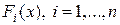 – заданные функции;
– заданные функции; 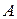 – матрица, не зависящая от x.
– матрица, не зависящая от x.
Общее решение задачи ( 31) определяется формулой:
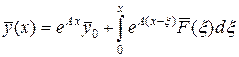 . ( 32)
. ( 32)
Пример 2. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида
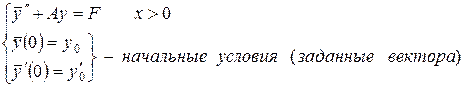 ( 33)
( 33)
Пусть 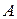 – положительно определенная матрица, т.е. все ее собственные числа
– положительно определенная матрица, т.е. все ее собственные числа 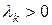 . Тогда общее решение ( 33) можно записать в виде:
. Тогда общее решение ( 33) можно записать в виде:
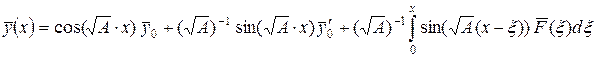 . ( 34)
. ( 34)
Пример 3. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида
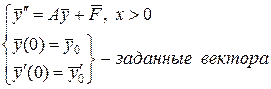 ( 35)
( 35)
Общее решение задачи ( 35) определяется формулой:
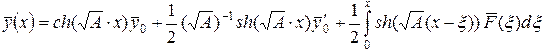 , ( 36)
, ( 36)
где 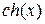 и
и 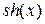 – гиперболические синус и косинус от произвольного аргумента.
– гиперболические синус и косинус от произвольного аргумента.
Замечание 3. В среде МАТЛАБ реализовано вычисление некоторых функций от матриц с помощью обращения к стандартной функции funm:
| Function | Syntax for Evaluating Function at Matrix A |
| exp | funm(A, @exp) |
| log | funm(A, @log) |
| sin | funm(A, @sin) |
| cos | funm(A, @cos) |
| sinh | funm(A, @sinh) |
| cosh | funm(A, @cosh) |
Кроме того, для вычисления 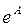 ,
, 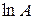 и
и 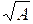 можно использовать встроенные функции expm(A), logm(A) и sqrtm(A), соответственно.
можно использовать встроенные функции expm(A), logm(A) и sqrtm(A), соответственно.
Дата добавления: 2016-12-26; просмотров: 546;
