Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности

Пространственная задача. Теория распределения в грунтовом пространстве напряжений, возникающих от действия сосредоточенной силы, представляют собой исходную теорию для расчета грунтовых оснований, нагруженных более сложными реальными нагрузками, распределенными на площади основания по разным закономерностям. Поэтому в начале мы рассматриваем приложение сосредоточенной силы к поверхности линейно-деформируемого однородного изотропного полупространства. Величина напряжений в любой точке полупространства была найдена французским ученым Буссинеском в 1885 г.

На схеме (рис.3.7) выделим точку М с полярными координатами R и b. Определим напряжения, действующие в точке М на площадку, перпендикулярную радиусу R. Для определения радиального напряжения s_R проделаем следующее: рассмотрим перемещение точки М в направлении радиуса R. Чем дальше от точки приложения внешней силы Р находится рассматриваемая точка М₁, тем меньше будет ее перемещение. При одной и той же величине R перемещения точек, соответствующих различным углам b, будут различны; наибольшее перемещение произойдет по оси z (при b=0), наименьшее - по оси y (при b = 90^о).

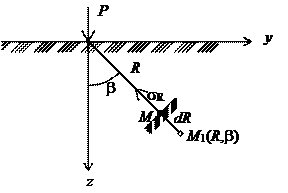
Рис.3.7. Схема деформации точки М в нагруженном полупространстве

Исходя из вышеизложенного, можно принять, что перемещение точки М в направлении радиуса R будет

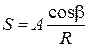, (3.6)

где A – неизвестный нам коэффициент пропорциональности.

Аналогично предыдущему, перемещение точки М₁, расположенной от точки М на расстоянии dR, будет

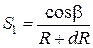. (3.7)

Относительная деформация отрезка dR выразится в виде

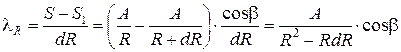. (3.8)

Пренебрежем величиной RdR, как ничтожно малой по сравнению с R², и тогда получим

.

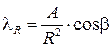Поскольку напряжения пропорциональны деформациям, мы можем написать выражение для радиального напряжения s_R в точке М:

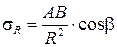, (3.9)

где B – неизвестный нам коэффициент пропорциональности.

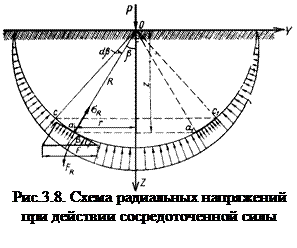Для определения коэффициентов А и В проведем полушаровое сечение радиусом R с центром в точке приложения внешней силы Р (рис.3.8). По поверхности полушара будут приложены радиальные напряжения s_R, переменность величины которых определяется только величиной угла b. Интенсивность напряжений s_R одинакова для каждого элементарного шарового пояса, отвечающего центральному углу db.

Из условий равновесия сумма проекций всех сил на вертикальную ось должна быть равна нулю

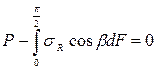, (3.10)

где dF – поверхность элементарного шарового пояса,

dF =2p(Rsinb)(Rdb). (3.11)

Подставляем значения dF в уравнение равновесия и решаем интеграл:

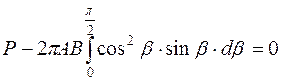. (3.12)

,

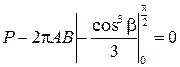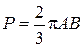, откуда .

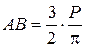Подставляя полученные значения коэффициентов АВ в формулу (3.9), получим

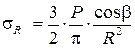. (3.13)

Пользуясь полученным выражением, можно найти напряжение в любой точке линейно-деформируемого массива, нагруженного с поверхности сосредоточенной силой Р.

В практике пользование радиальными напряжениями неудобно, т.к. направление их в разных точках массива различно. Поэтому радиальное напряжение выражают через составляющие по площадкам, нормальным к осям координат x,y,z, при расположении координатной системы, как показано ниже. Отнесем величину радиального напряжения s_R к горизонтальной площадке, параллельной ограничивающей плоскости (рис.3.9):

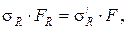
а так как 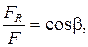то величина радиального напряжения, отнесенного к горизонтальной площадке, равна

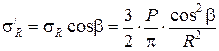. (3.14)

Проектируя величину 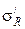по трем взаимно перпендикулярным направлениям и учитывая, что cosb=z/R, получим составляющие напряжения для любой площадки, параллельной ограничивающей плоскости:

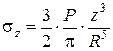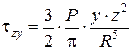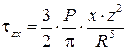, , . (3.15)

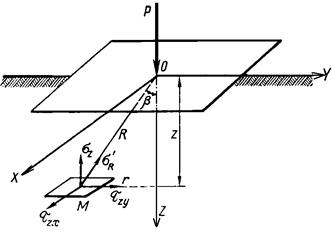
Рис.3.9. Отнесение радиального напряжения к горизонтальной площадке

Составляющие напряжения для площадок, перпендикулярных осям x и y, имеют несколько более сложный вид и зависят от величины коэффициента бокового расширения n₀ и модуля деформации Е₀.

Наибольшее практическое значение имеют напряжения, действующие на площадке, параллельной ограничивающей плоскости, особенно нормальная составляющая s_z, вызывающая уплотнение грунта. Учитывая, что полярные координаты b и R можно выразить через прямоугольные координаты x, y, z, уравнение для s_z может быть приведено к виду

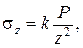(3.16)

где k – коэффициент, зависящий от положения рассматриваемой точки в пространстве,

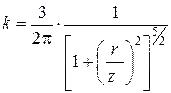, (3.17)

где r – расстояние рассматриваемой точки от вертикальной оси приложения нагрузки. Значения k табулированы в зависимости от отношений r/z (табл. II.1 приложения II, пример 1).

Если на поверхности массива действует несколько сосредоточенных сил P₁, P₂, P₃ (рис.3.10), то сжимающее напряжение в любой точке массива можно найти простым суммированием:

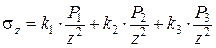, (3.18)

где коэффициент 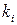определяют по табл. в зависимости от соотношений r_i/z (табл. II.1 приложения II).

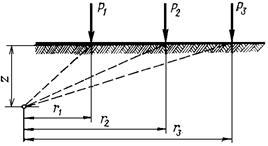
Рис.3.10. Схема действия нескольких сосредоточенных сил

Если на поверхности массива приложена местная равномерно распределенная нагрузка на площади ограниченных размеров, то напряжения в любой точке массива могут быть найдены по принципу независимости действия сил как сумма напряжений, возникающих от сосредоточенных нагрузок, заменяющих действие равномерно распределенной нагрузки на элементарных площадках и приложенных в центре тяжести последних (рис.3.11) (пример 2).

Рис.3.11. Схема замены действия равномерно распределенной нагрузки элементарными сосредоточенными силами

Определив величину s_zi от нагрузки каждой площадки, на которые разбита загруженная площадь, и произведя суммирование этих напряжений, найдем напряжение s_z от действия распределенной нагрузки:

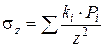. (3.19)

Этот приближенный метод может быть заменен точным интегрированием по всей площади напряжений от нагрузки на бесконечно малый элемент загруженной площади.

Точные решения этой задачи имеют очень сложный вид. В настоящее время получены формулы для определения напряжений под центром загруженного прямоугольника:

max 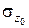=k₀P (3.20)

и для площадок под углом загруженного прямоугольника

s_zc= k_cP, (3.21)

где k₀ и k_c – табличные коэффициенты, табулированные в зависимости от отношения сторон прямоугольной площадки загрузки a=l/b и относительной глубины рассматриваемой точки 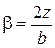(l – длина прямоугольника, b – ширина). Для угловой точки 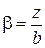(табл. II.2 приложения II, пример 3)

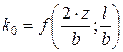, (3.22)

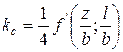. (3.23)

Из формулы (3.23) видно, что угловые напряжения составляют 0,25 от напряжений под центром загруженной площадки.