Проектируем все силы на наклонную грань откоса с учетом
Устойчивость откосов и склонов
При разработке котлованов, вертикальной планировке площадок с уступами, устройстве выемок и насыпей, возведении сооружений на склонах и в ряде других случаев приходится оценивать устойчивость массивов грунтов в откосах. Устройство пологих откосов резко удорожает строительство. Крутые откосы могут привести к аварии. Нужно находить оптимальные крутизны откосов или проектировать подпорные стенки.
Причины потери устойчивости откосов:
- устранение естественной опоры массива грунта вследствие разработки котлованов, траншей и т.д.;
- увеличение внешней нагрузки на откос;
- увеличение удельного веса грунта в призме обрушения в результате насыщения пор водой;
- влияние капиллярной влаги при понижении уровня грунтовых вод;
- снижение сцепления и трения грунта при увлажнении, промерзании и оттаивании грунтов;
- динамические воздействия (движение транспорта, сейсмические проявления);
- большая крутизна откосов.
Нарушение равновесия массива грунта может происходить внезапно со сползанием значительных масс грунта. Такие нарушения равновесия называются оползнями. Оползни бывают следующих видов:
а) оползни вращения (с криволинейными поверхностями обрушения);
б) оползни скольжения (по зафиксированным поверхностям);
в) оползни разжижения (грязевые потоки перенасыщенных водой грунтов).
4.5.1. Устойчивость откосов идеально сыпучего грунта (с=0, j¹0)
Пусть имеется откос с углом заложения a при заданном значении угла внутреннего трения j песка, слагающего откос.
Рассмотрим равновесие частицы грунта М, свободно лежащей на поверхности откоса (рис.4.13,а). Вес частицы Р разложим на нормальную N к линии ab и касательную Т, стремящуюся сдвинуть частицу вниз. Грунт обладает только внутренним трением, поэтому устойчивость частицы будет обеспечена, если сдвигающая сила Т равна удерживающей силе трения Т '=fN или меньше нее.
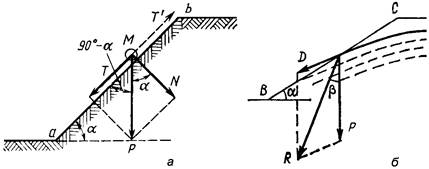 |
Рис.4.13. Схема к расчету устойчивости откосов сыпучего грунта:
а – сухого; б – фильтрующего воду
Проектируем все силы на наклонную грань откоса с учетом
N = Pcosa, T = Psina, Psina – fPcosa = 0. (4.30)
Отсюда tga=f , а т.к. коэффициент трения f=tgj, то получаем a=j. Следовательно, предельный угол откоса сыпучих грунтов равен углу внутреннего трения. Этот угол носит название угла естественного откоса.
Для обеспечения устойчивости откоса сила, удерживающая частицы М, должна быть больше сдвигающих сил: T 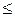 T '. Примем за коэффициент надежности gn, тогда gntga£tgj . Обычно gn принимают равным 1,1¸1,2.
T '. Примем за коэффициент надежности gn, тогда gntga£tgj . Обычно gn принимают равным 1,1¸1,2.
Если уровень подземных вод в массиве сыпучих грунтов находится выше подошвы откоса, возникает фильтрационный поток,выходящий на поверхность откоса. В грунте появляется гидродинамическое давление, что приводит к снижению устойчивости откоса. Поэтому рассматривая равновесие частицы М на поверхности откоса, к сдвигающей силе необходимо добавить гидродинамическую составляющую
D = gwni, (4.31)
где gw – удельный вес воды; n – пористость грунта, i – градиент напора.
В точке выхода воды через поверхность откоса действуют силы D и P, которые приводятся к равнодействующей R, отклоняющейся от вертикали на угол b. В этом случае устойчивость угла откоса находим из условия
gntga £ tg(j-b). (4.32)
4.5.2. Устойчивость вертикального откоса грунта, обладающего только сцеплением (j=0,c¹0)
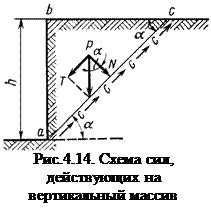 Рассмотрим для такого грунта устойчивость вертикального откоса ab высотой h (рис.4.14). Проведем линию ас возможной поверхности скольжения под углом a к горизонту. По всей этой плоскости будут действовать удельные силы сцепления.
Рассмотрим для такого грунта устойчивость вертикального откоса ab высотой h (рис.4.14). Проведем линию ас возможной поверхности скольжения под углом a к горизонту. По всей этой плоскости будут действовать удельные силы сцепления.
Составим уравнение равновесия всех сил, действующих на оползающую призму abc. Действующей силой будет вес Р призмы abc.
Учитывая, что bc=hctga, получаем
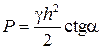 . (4.33)
. (4.33)
Силу Р разложим на нормальную N и касательную Т составляющие к поверхности скольжения ас. Силами, сопротивляющимися скольжению, будут лишь силы сцепления с, распределенные по плоскости скольжения 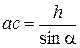 .
.
Так как в верхней точке с призмы abc давление равно нулю, а в нижней а оно максимально, то в среднем следует учитывать лишь половину сил сцепления.
Составим уравнение равновесия, взяв сумму проекций всех сил на направление ас и приравняв ее нулю:
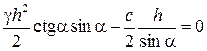 , (4.34)
, (4.34)
откуда
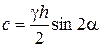 . (4.35)
. (4.35)
Определим значение высоты h=h90, соответствующей максимальному использованию сил сцепления. Очевидно, при этом sin2a=1, a=450. Тогда, подставляя sin2a=1 в выражение (4.35) и решая его относительно h90, получим
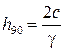 . (4.36)
. (4.36)
При коэффициенте надежности gn имеем
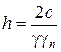 . (4.37)
. (4.37)
В данном случае h – максимально возможная высота откоса без крепления.
4.5.3. Устойчивость откосов по теории предельного равновесия
Для грунтов, обладающих и внутренним трением и сцеплением, В.В.Соколовским решены две задачи:
1. Определение максимального давления на горизонтальную поверхность массива грунта, при которой откос данного очертания остается в равновесии.
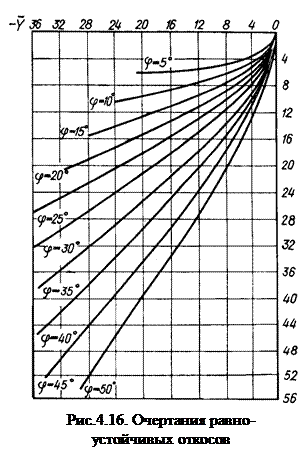
2. Определение формы равноустойчивого откоса предельной крутизны.
На основании численного интегрирования дифференциальных уравнений предельного равновесия при различных углах внутреннего трения j и углах наклона плоского откоса к горизонту a можно найти предельные значения Р:
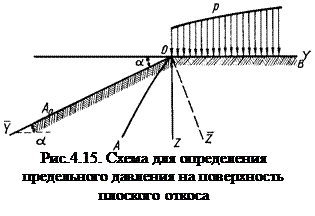
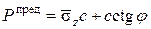 , (4.38)
, (4.38)
где 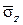 – безразмерная величина предельного давления (табл.III.5 приложения III), принимается в зависимости от j, a и относительной координаты
– безразмерная величина предельного давления (табл.III.5 приложения III), принимается в зависимости от j, a и относительной координаты 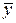 :
:
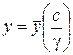 ,
, 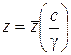 . (4.39)
. (4.39)
Очертания равноустойчивого откоса строят, начиная с его верхней кромки.
Горизонтальная поверхность равноустойчивого откоса может нести равномерно распределенную нагрузку
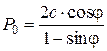 . (4.40)
. (4.40)
Если P0 рассмотреть как давление слоя грунта Р0 = gh , то
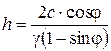 . (4.41)
. (4.41)
При j = 0 h = 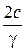 .
.
4.5.4. Расчет устойчивости откосов приближенным методом круглоцилиндрических поверхностей скольжения
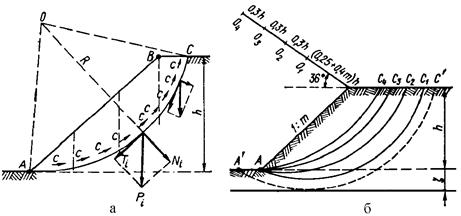
Этот метод, широко используемый в практике, впервые был применен К.Петерсоном в 1916 г. и долгое время назывался "методом шведского геотехнического общества". Сущность применения метода сводится к следующему. Задаются центром вращения О откоса АВ. Уравнением равновесия будет SМ0=0. Для составления уравнения моментов относительно точки вращения О разбиваем призму скольжения АВС вертикальными сечениями на ряд отсеков и принимаем вес каждого отсека условно приложенным к точке пересечения веса отсека Pi с соответствующим отрезком дуги скольжения. Раскладываем силы веса Pi на направление радиуса вращения и ему перпендикулярное (рис.4.17,а) и составляем уравнение равновесия, приравнивая нулю момент всех сил относительно точки вращения:
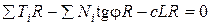 . (4.42)
. (4.42)
Сокращая это выражение на R, получим
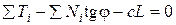 , (4.43)
, (4.43)
 |
где L – длина дуги скольжения; c, j – угол внутреннего трения и сила сцепления; Ti и Ni – соответственно касательная и нормальная составляющие силы веса:
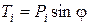 ,
, 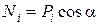 .
.
Рис.4.17. Схемы расчета устойчивости откосов по круглоцилиндрическим поверхностям скольжения: а – схема действия сил; б – положение опасных дуг скольжения
За коэффициент устойчивости откоса принимают отношение момента сил удерживающих к моменту сил сдвигающих:
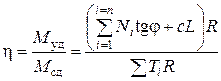
или (4.44) 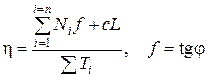 .
.
Необходимо из всех возможных дуг поверхностей скольжения выбрать наиболее опасную (рис.4.17,б). Для намеченных центров дуг О1, О2, О3 определяем необходимое по условию устойчивости сцепление, соответствующее предельному равновесию,
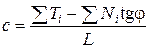 . (4.45)
. (4.45)
Из всех возможных центров скольжения выбираем тот, для которого требуется максимальная величина сил сцепления. Коэффициент устойчивости h принимаем равным 1,1…1,5. Изложенный метод уточнен М.Н.Гольдштейном и Г.И.Тер-Степаняном:
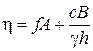 , (4.46)
, (4.46)
где А и В – коэффициенты (табл.III.6 приложения III, пример 8), табулированные в зависимости от соотношения заложения откоса m и x=(0,25; 0,5; 1,0; 1,5)h
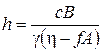 . (4.47)
. (4.47)
4.5.5. Устойчивость прислоненных откосов и склонов
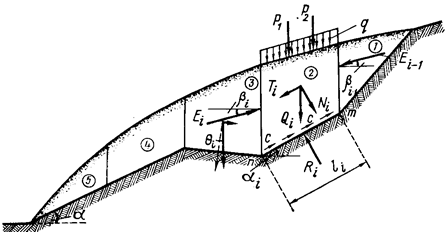 |
Устойчивость прислоненного откоса определяется из уравнений равновесия. При этом разбивают массив грунта на ряд отсеков так, чтобы в пределах отдельных отсеков поверхность скольжения была плоской и проходила по фиксированной поверхности более плотных ненарушенных пород (рис.4.18).
Рис.4.18. Схема действия сил при определении оползневого давления
При рассмотрении i-го отсека учитывают все внешние силы, включая нагрузку, приложенную к поверхности отсека, и вес грунта в объеме отсека. Сумму внешних сил Qi раскладывают на нормальную Ni и касательную Тi. Нормальная сила Ni позволяет учитывать силы трения по основанию nm. Кроме того, учитывают силы сцепления при сдвиге по этой плоскости. Дополнительно на отсек действует неуравновешенное оползневое давление от вышележащих отсеков Еi-1 и неизвестное оползневое давление на нижележащий отсек Еi. Если откос подвержен еще действию сейсмических сил, отклоняющих равнодействующую внешних сил от вертикали на некоторый угол qi, то получим
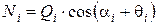 и
и 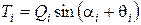 . (4.48)
. (4.48)
По уравнениям равновесия – сумме проекций всех сил на направление nm и нормаль к этому направлению – можно найти значение оползневого давления Еi, передаваемого на следующий отсек:
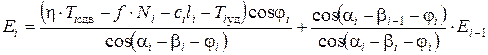 ,
,  (4.49)
(4.49)
где h – коэффициент устойчивости.
Расчет начинают с первого верхнего отсека, для которого Еi-1=0. Переходя от отсека к отсеку, достигают последнего отсека, который должен быть устойчивым при En £ 0.
4.5.6. О мерах борьбы с оползнями
Нарушение устойчивости земляных масс сопровождается разрушением дорог, мостов, жилых и промышленных зданий, иногда с человеческими жертвами.
К мерам по увеличению устойчивости массивов грунта и борьбе с оползнями относятся:
- восстановление и усиление естественных упоров оползающих масс;
- регулирование водного режима грунтовых масс;
- уменьшение нагрузок.
| <== предыдущая лекция | | | следующая лекция ==> |
| АЛЬТЕРНАТИВНЫЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ | | | КЛИНИКА И ДИАГНОСТИКА ГЕСТОЗА |
Дата добавления: 2016-05-11; просмотров: 2312;
