Перетворення Лапласа

Динамічні властивості автоматичних систем та їх складових частин (ланок) математично описуються диференціальними рівняннями. Чим більше в системі нагромаджуючих елементів, тим вище порядок диференціального рівняння, що зв’язує вихідну і вхідну величини системи.

Розв’язок лінійних диференціальних рівнянь може бути спрощений при використанні методів, що базуються на перетворенні функцій дійсної змінної у функції комплексної змінної. Методи функціонального перетворення дозволяють інтегро-диференціальні рівняння заміняти алгебраїчними рівняннями, розв’язок яких є значно простіший. Практичне використання знайшли методи перетворення Лапласа.

Перехід від функції дійсної змінної до функції комплексної змінної називається прямим перетворенням Лапласа і описується рівнянням:

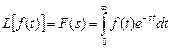(4.1)

де 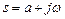комплексна змінна.

У виразі (4.1) функція f(t) називається оригіналом, а функція F(s) – зображенням. Зворотний перехід від зображення до оригіналу можна здійснити за зворотним перетворенням Лапласа:

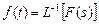(4.2)

На практиці не доводиться обчислювати інтеграли прямого й зворотного перетворення Лапласа. При складанні рівнянь динаміки широко використовується операторна форма запису диференціальних рівнянь, згідно з якою вводяться символи похідних і інтегралів, що визначаються за допомогою оператора р.

Символ диференціювання за часом d/dt замінюють оператором р, а операцію інтегрування – оберненою величиною оператора 1/р.

Записуємо похідні в операторній формі:

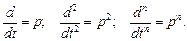
Тоді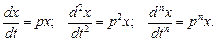

Записуємо інтеграли в операторній формі:

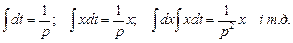
При переході до операторної форми запису диференціальні рівняння перетворюються в алгебраїчні і їх розв’язують звичайними алгебраїчними діями (додаванням, відніманням, діленням і множенням), а не більш складними – інтегруванням і диференціюванням.

Правомірність відокремлення функції від знака оператора можна показати на основі відомих положень математики. Наприклад, на основі того, що похідна суми деяких величин x, y, z є сума цих похідних

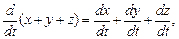
в операторній формі можна записати: px+py+pz=p(x+y+z).

Для спеціальних функцій перехід від оригіналів до зображень і навпаки здійснюють за допомогою таблиць перетворення Лапласа, які є в спеціальній літературі.