Многогранники и их изображение

Напомним определения многогранника и некоторых его видов.

Многогранник - это ограниченное тело, поверхность которого со­стоит из конечного числа многоугольников. Выпуклый многогранник лежит по одну сторону от каждого из ограничивающих его много­угольников. Многоугольник на поверхности многогранника называ­ется его гранью. Стороны граней называются ребрами многогранника, а вершины граней - вершинами многогранника.

Простейшие многогранники - это призма и пирамида. Призмой на­зывается многогранник, у которого две грани, называемые основа­ниями призмы, равны и их соответственные стороны параллельны, а остальные грани - параллелограммы, у каждого из которых две сто­роны являются соответственными сторонами оснований.

Призма называется прямой, если ее боковые ребра перпендикуляр­ны основанию.

Прямая призма называется правильной, если ее основанием являет­ся правильный многоугольник.

Призма, у которой основание - параллелограмм, называется па­раллелепипедом.

Параллелепипед называется прямоугольным, если все его грани -прямоугольники.

Куб - это прямоугольный параллелепипед, все ребра которого равны, т.е. все грани которого - квадраты.

Изобразим, например, наклонную призму, основанием которой являются квадраты.

Построим сначала нижнее основание призмы (можно начинать и с верхнего). По правилам параллельного проектирования оно изобразится

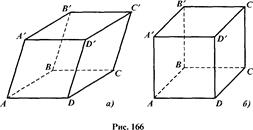
произвольным параллелограммом АВСD (рис. а). Так как ребра призмы параллельны, строим параллельные прямые, проходя­щие через вершины построенного параллелограмма и откладываем на них равные отрезки АА', ВВ', СС', ВВ'', длина которых произвольна. Соединив последовательно точки А', В', С', D', получим четырех­угольник А'В'С'D', изображающий верхнее основание призмы. Не­трудно доказать, что А'В'С'D' - параллелограмм, равный параллело­грамму АВСD и, следовательно, мы имеем изображение призмы, ос­нованиями которой являются равные квадраты, а остальные грани -параллелограммы.

Если нужно изобразить прямую призму, основаниями которой яв­ляются квадраты, то показать, что боковые ребра этой призмы перпен­дикулярны основанию, можно так, как это сделано на рисунке б.

Кроме того, чертеж на рисунке б можно считать изображени­ем правильной призмы, так как ее основанием является квадрат - правильный четырехугольник, а также - прямоугольным параллеле­пипедом, поскольку все его грани - прямоугольники.

Выясним теперь, как изобразить на плоскости пирамиду.

Пирамидой называется многогранник, у которого одна грань (ее называют основанием) - какой-нибудь многоугольник, а остальные грани (их называют боковыми) - треугольники с общей вершиной.

Общую вершину боковых граней называют вершиной пирамиды. Перпендикуляр, опущенный из вершины пирамиды на плоскость ее основания, а также длина этого перпендикуляра называется высотой пирамиды.

Простейшей пирамидой является треугольная пирамида - тетра­эдр. У нее наименьшее возможное число граней - всего четыре. Любая ее грань может считаться основанием, что и отличает тетраэдр от других пирамид.

Пирамида называется правильной, если ее основание - правильный многоугольник и высота проходит через центр этого многоугольника.

Чтобы изобразить правильную пирамиду, сначала чертят правиль­ный многоугольник, лежащий в основании, и его центр - точку О. Затем проводят вертикальный отрезок ОS, изображающий высоту пи­рамиды. Заметим, что вертикальность отрезка ОS обеспечивает боль­шую наглядность рисунка. И наконец, точку S соединяют со всеми вер­шинами основания.

Изобразим, например, правильную пирамиду, основанием которой является правильный шестиугольник.

Чтобы верно изобразить при параллель­ном проектировании правильный шести­угольник, надо обратить внимание на сле­дующее. Пусть АВСDЕF - правильный шес­тиугольник. Тогда ВСЕF - прямоугольник (рис.) и, значит, при параллельном про­ектировании он изобразится произвольным параллелограммом В'С'Е'F'. Так как диаго­наль АD проходит через точку O - центр мно­гоугольника АВСDЕF и параллельна отрезкам ВС и ЕF и АО = ОD, то при параллельном проектировании она изобра­зится произвольным отрезом А'D', проходящим через точку О' парал­лельно В'С' и Е'F' и, кроме того, А'О' = 0'D'.

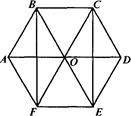
Таким образом, последовательность построения основания шести­угольной пирамиды такова (рис.):

- изображают произвольный параллелограмм В'С'Е'F' и его диагонали; отмечают точку их пересечения О';

- через точку О' проводят прямую, па­раллельную В'С' (или Е'F');

- на построенной прямой выбирают про­извольную точку А' и отмечают точку D' такую, что 0'D' = А'О', и соединяют точку А' с точками В' и F' , а точку D' с точками С' и Е'.

Чтобы завершить построение пирамиды, проводят вертикальный отрезок OS (его длина выбирается произвольно) и соединя­ют точку Sсо всеми вершинами основания.

Завершая рассмотрение многогранников, отметим еще их одно ин­тересное свойство, установленное Л. Эйлером.

Теорема Эйлера. Пусть дан выпуклый многогранник и В - число его вершин, Р - число ребер, Г - число граней. Тогда В + Г - Р== 2 для любого выпук­лого многогранника. Например, правильная шестиугольная пира­мида имеет 7 вершин (В = 7), 12 ребер (Р = 12) и 7 граней (Г = 7). Тог­да В + Г - Р= 7 - 12 + 7 = 2. На основании теоремы Эйлера можно заключить, что существует пять и только пять видов правильных многогранников, т.е. таких выпуклых многогранников, у которых все грани - равные друг другу правильные многоугольники и в каж­дой его вершине сходится одно и то же число ребер. Это - тетраэдр, куб, октаэдр, икосаэдр, додекаэдр (рис.).