Элементарные задачи на построение

С помощью основных построений решаются некоторые задачи, достаточно простые и часто встречающиеся при решении других, бо­лее сложных. Такие задачи считаются элементарными и описания их решения, если они встречаются при решении более сложных, не дается. Выбор элементарных задач является условным.

Задача на построение считается решенной, если указан способ построения фигуры и доказано, что в результате выполнения ука­занных построений действительно получается фигура с требуемыми свойствами.

Рассмотрим некоторые элементарные задачи на построение.

1. Построить на данной прямой отрезок СD, равный данному от­резку АВ

Возможность такого построения вытекает из аксиомы откладыва­ния отрезка. С помощью циркуля и линейки оно осуществляется сле­дую щим образом. Пусть даны прямая а и отрезок АВ. Отмечаем на прямой точку С и строим с центром в точке С окружность радиусом, равным отрезку АВ. Точку пересечения окружности с прямой а обо­значаем D. Получаем отрезок СD, равный АВ.

2. Отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.

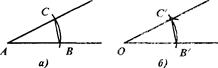
Пусть даны угол А и по­лупрямая с начальной точ­кой О. Проведем окружность произвольного радиуса с цент­ром в вершине А данного угла (рис. а). Точки пересече­ния окружности со сторонами угла обозначим В и С. Радиусом АВ проведем окружность с центром в точке О (рис. б). Точку пере­сечения этой окружности с данной полупрямой обозначим В'. Опи­шем окружность с центром В' и радиусом ВС. Точка С' пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.

Построенный угол В'ОС' равен углу ВАС, так как это соответст­вующие углы равных треугольников АВС и В'ОС.

3. Найти середину отрезка.

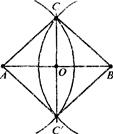
Пусть АВ - данный отрезок. Построим две окружности одного радиуса с центрами А и В (рис.). Они пересекаются в точках С и С', лежащих в разных полуплоскостях относитель­но прямой АВ. Проведем прямую СС'. Она пе­ресечет прямую АВ в точке О. Эта точка и есть середина отрезка АВ.

Действительно, треугольники САС' и СВС' равны по трем сторонам. Отсюда следует равен­ство углов А СО и ОСВ. Значит, отрезок СО -биссектриса равнобедренного треугольника АСВ и, следовательно, его медиана, т.е. точка О - се­редина отрезка АВ.

4. Построить биссектрису данного угла.

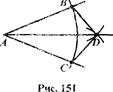
Из вершины А данного угла как из центра описываем окружность произвольного радиуса (рис.). Пусть В и С- точки ее пересечения

со сторонами угла. Из точек В и С описываем окружности одного радиуса. Пусть В - точка их пересечения, отличная от А. Тогда по­лупрямая АО и есть биссектриса угла А. Докажем это. Для этого рассмотрим треугольники АВD и АСВ. Они равны по трем сторо­нам. Отсюда следует равенство соответствующих углов DАВ и ВАС, т.е. луч АD делит угол ВАС пополам и, следовательно, является бис­сектрисой.

5. Через данную точку провести прямую, перпендикулярную дан­ной прямой.

Пусть даны точка О и прямая а. Возможны два случая:

1) точка О лежит на прямой а;

2) точка О не лежит на прямой а.

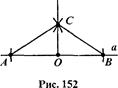
В первом случае построение выполняется так же, как и в задаче 4, потому что перпенди­куляр из точки О, лежащей на прямой, - это биссектриса развернутого угла (рис.).

Во втором случае из точки О как из центра проводим окружность, пересекающую прямую а (рис.), а затем из точек А и В тем же ра­диусом проводим еще две окружности. Пусть О' - точка их пересечения, лежащая в полу­плоскости, отличной от той, в которой лежит точка О. Прямая 00' и есть перпендикуляр к данной прямой а. Докажем это.

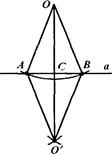
Обозначим через С точку пересечения пря­мых АВ и 00'. Треугольники АОВ и АО'В равны по трем сторонам. Поэтому угол ОАС равен углу О'АС и, значит, треугольники ОАС и О'АС равны по двум сторонам и углу между ними. Отсюда их углы АСО и АСО' равны. А так как углы смежные, то они прямые. Таким образом, ОС есть пер­пендикуляр к прямой а.

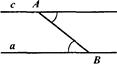
6. Через данную точку провести прямую, параллельную данной. Пусть даны прямая а и точка А вне этой прямой (рис.). Возь­мем на прямой а какую-нибудь точку В и соединим ее с точкой А. Через точку А проведем прямую с, образующую с АВ такой же угол, какой АВ образует с дан­ной прямой а, но на противоположной стороне от АВ. Построенная прямая будет параллельна прямой а, что следует из равенства накрест ле­жащих углов, образованных при пересечении прямых а и с секущей АВ.

Упражнения

1. Постройте с помощью циркуля и линейки сумму и разность двух данных: а) отрезков; б) углов.

2. Разделите данный угол на 4 равных части.

3. Дан треугольник АВС. Постройте другой, равный ему, треуголь­ник АВD.

4. Постройте окружность данного радиуса, проходящую через две данные точки.