Равномощные множества. Способы установления равномощности множеств. Счетные и несчетные множества.
Определение. Множества X и Y называются равномощными, если между ними можно установить взаимно однозначное соответствие.
Если множества X и Y равномощны, то пишут X ~ Y.
Нетрудно увидеть, что множества, которые были рассмотрены в примерах 1 и 2, равномощны.
Равномощными могут быть как конечные, так и бесконечные множества. Равномощные конечные множества называют еще равночисленными. В начальном обучении математике равночисленность выражается словами «столько же» и может использоваться при ознакомлении учащихся со многими другими понятиями. Например, чтобы ввести равенство чисел, сравнивают два множества, устанавливая между их элементами взаимно однозначное соответствие. Например, пишут, что 5 = 5, так как кружков столько же, сколько квадратов (рис. 76).
Понятие равночисленности множеств лежит и в основе определения отношений «больше на ...» и «меньше на ...». Например, чтобы утверждать, что 6 больше 4 на 2, сравнивают два множества, устанавливая взаимно однозначное соответствие между множеством X, в котором 4 элемента, и подмножеством Y, другого множества Y, в котором 6 элементов (рис. 77), и делают вывод: треугольников столько же, сколько кружков, и еще 2. Другими словами, треугольников на 2 больше, чем кружков.
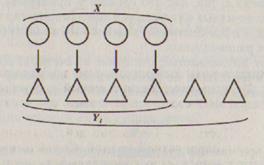
Рис. 77
Как уже было сказано, равномощными могут быть и бесконечные множества. Приведем примеры таких множеств.
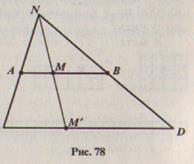
Пример 3. Пусть X - множество точек отрезка АВ, Y - множество точек отрезка СD, причем длины отрезков различны. Так как между данными множествами можно установить взаимно однозначное соответствие (рис. 78), то множества точек отрезка АВ и СD равномощны.
Пример 4. Рассмотрим множество Nнатуральных чисел и множество Y - четных натуральных чисел. Они равномощны, так как между их элементами можно установить взаимно однозначное соответствие:



 N: 1 2 3 … n …
N: 1 2 3 … n …
Y: 2 4 6 … 2n …
На первый взгляд кажется парадоксальным тот факт, что можно установить взаимно однозначные соответствия между множеством и его частью: для конечных множеств такая ситуация невозможна. Однако в математике доказано, что для бесконечного множества А всегда найдется такое его подмножество B, что между А и В можно установить взаимно однозначное соответствие. Иногда это утверждение считают определением бесконечного множества.
Если бесконечное множество равномощно множеству N натуральных чисел, его называют счетным. Любое бесконечное подмножество множества N счетно: чтобы пронумеровать его элементы, надо расположить элементы подмножества в порядке возрастания и нумеровать один за другим (т.е. так, как это сделано в примере 4). Так, счетно множество всех нечетных натуральных чисел, множество натуральных чисел, кратных 5 и др. Счетными являются также множества всех целых чисел, всех рациональных.
Существуют ли множества, отличные от счетных? Доказано, что бесконечным множеством, не равномощным множеству N натуральных чисел, является множество R всех действительных чисел.
Упражнения
1.Задайте при помощи графа три соответствия между множествами X = {а, b, с} и Y = {2, 4, 6} так, чтобы одно из них было взаимно однозначным.
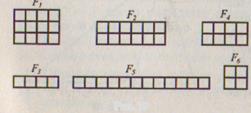
Рис.79
2.X - множество прямоугольников (рис. 79), Y = N. Между элементами этих множеств установлено соответствие Р: «прямоугольник х имеет площадь, равную у». Постройте граф соответствия Р. Является ли оно взаимно однозначным?
3.Как можно изменить множества X и Y, данные в упражнении 2, чтобы соответствие Р: «прямоугольник х имеет площадь, равную у», было взаимно однозначным?
4.Даны множества: А = {1, 2, 5}, В = {3, 7}. Найдите А х В и В х А. Верно ли, что найденные множества равномощны?
5.Докажите, что множество А счетно, если:
а) А = {9,10,11,12,...};
б) А = (а│а = 3n, n € N};
 в) А = {а│а = n2, n € N}.
в) А = {а│а = n2, n € N}.
6. Покажите, что, выполняя нижеприведенные задания, учащиеся начальных классов используют понятие равночисленности множеств:
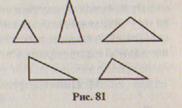
|
а) Нарисуй на другой фигуре (рис. 80) столько же точек, сколько на первой (точки не пересчитывать).
б) Нарисуй, не считая, столько же квадратов и столько же отрезков, сколько на рисунке 81 треугольников.
в) У Димы было 28 марок, а у Коли на 7 марок больше. Сколько марок было у Коли?
г) У Маши 9 игрушек, а у Риты на 2 меньше. Сколько игрушек у Риты?
д) Для детского сада купили 4 зеленых мяча, а красных в 3 раза больше, чем зеленых. Сколько красных мячей купили детям?
е) Для детского сада купили 15 красных мячей, а зеленых в 3 раза меньше. Сколько зеленых мячей купили детям?
43. Основные выводы § 8
Изучая материал этого параграфа, мы установили, что любое соответствие S между двумя множествами X и Y есть подмножество декартова произведения этих множеств, т.е. S с X х Y. Выяснили, что соответствия задают также, как и множества вообще. Познакомились с новыми понятиями:
- соответствие, обратное данному;
- взаимно однозначное соответствие;
- равномощные множества;
- счетное множество.
Установили, что графики взаимно обратных соответствий между числовыми множествами симметричны относительно биссектрисы 1-го и 3-го координатных углов.
Дата добавления: 2016-05-11; просмотров: 4636;
