Лекция17. Взаимно-однозначные соответствия

План:

1. Взаимно-однозначные соответствия. Понятие взаимно однозначного отображения множества Х на множество Y.

2. Равномощные множества. Способы установления равномощности множеств. Счетные и несчетные множества.

3. Основные выводы

Взаимно однозначные соответствия. Понятие взаимно однозначного отображения множества Х на множество Y

В математике изучают различные виды соответствий. Это не слу­чайно, поскольку взаимосвязи, существующие в окружающем нас мире, многообразны. Для учителя, обучающего математике младших школьников, особую значимость имеют взаимно однозначные соот­ветствия.

Определение. Взаимно однозначным соответствием между множествами X и Y называется такое соответствие, при кото­ром каждому элементу множества X сопоставляется единст­венный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества X.

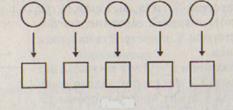
Рис. 76

Это соответствие взаимно однозначное, так как каждому кружку из множества X сопоставляется единственный квадрат из множества Y и каждый квадрат из Y соответствует только одному кружку из множества X.

Пример 2. Пусть X - множество действительных чисел, Y - множество точек координатной прямой.Соответствие между ними таково: действительному числу сопоставляется точка координатной прямой. Это соответствие взаимно однозначное, так как каждому действительному числу сопоставляется единственная точка коорди­натной прямой и каждая точка на прямой соответствует только од­ному числу.

В математике взаимно однозначное соответствие между множествами X и Y часто называют взаимно однозначным отображение множества X на множество Y.

Понятие взаимно однозначного соответствия позволяет определитьотношение равномощности множеств.