И способы их расчета.
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним.
Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них - размах вариации.
Размах вариации - это разность между наибольшим ( 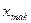 ) и наименьшим (
) и наименьшим ( 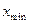 ) значениями вариантов.
) значениями вариантов.
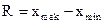
Пример 1.
Группы предприятий по объему товарооборота, млн.руб. 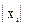
| Число предприятий 
|
| 90 — 100 | |
| 100 — 110 | |
| 110 — 120 | |
| 120 — 130 | |
| ИТОГО |
Определяем показатель размаха вариации:
R = 130 - 90 = 40 млн. руб.
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.
Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:
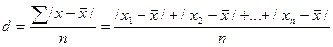 .
.
Пример 2.
| Табельный номер рабочего | 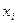 (кол-во деталей задень) (кол-во деталей задень)
| 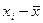
| / 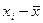 / /
|
| - 8 | |||
| - 7 | |||
| Итого |
d= 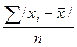 =
= 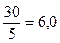
Это означает, что каждое значение признака отличается от своей средней величины на 6.
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:
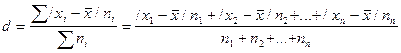
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается 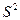 . В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
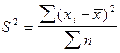 — дисперсия невзвешенная (простая);
— дисперсия невзвешенная (простая);
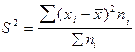 — дисперсия взвешенная.
— дисперсия взвешенная.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S:
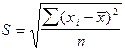 — среднее квадратическое отклонение невзвешенное;
— среднее квадратическое отклонение невзвешенное;
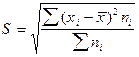 — среднее квадратическое отклонение взвешенное.
— среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Пример 3.
Произведено продукции одним рабочим, шт.
( 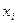 варианта) варианта)
| Число рабочих, 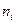
| 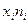
| 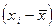
| 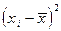
| 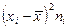
|
| -2 | |||||
| -1 | |||||
| ИТОГО |
Исчислим среднюю арифметическую взвешенную:
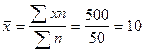 шт.
шт.
Значения отклонений от средней и их квадратов представлены в таблице 6.3. Определим дисперсию:
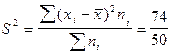 =1,48
=1,48
Среднее квадратическое отклонение будет равно:
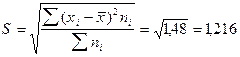 шт.
шт.
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить дискретное значение признака, а далее применить тот же метод, что изложен выше.
Пример 4.
Покажем расчет дисперсии для интервального ряда на данных о распределении посевной площади колхоза по урожайности пшеницы:
| Урожайность пшеницы, ц/га | Посевная площадь, га | 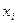
| 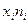
| 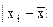
| 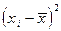
| 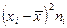
|
| 14 - 16 | -3,4 | 11,56 | ||||
| 16 - 18 | -1,4 | 1,96 | ||||
| 18 - 20 | 0,6 | 0,36 | ||||
| 20 - 22 | 2,6 | 6,76 | ||||
| ИТОГО |
Средняя арифметическая равна:
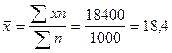 ц с 1га.
ц с 1га.
Исчислим дисперсию:
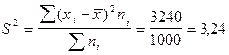
Коэффициент вариации.
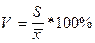 (3)
(3)
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. При этом исходят из того, что если V больше 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности.
Дата добавления: 2016-11-28; просмотров: 997;
