Средняя гармоническая.
Наряду со средней арифметической, в статистике применяется средняя гармоническая величина. Она применяется в тех случаях, когда статистическая информация не содержит частот по отдельным вариантам, а представлена как их произведение. Как и средняя арифметическая, она может быть простой и взвешенной.
Пример 6.
Бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.
На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:
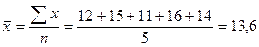
Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением:
все затраченное время
Среднее время, затраченное = --------------------------------------
на одну деталь число деталей
Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:
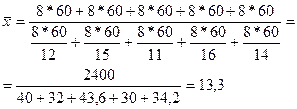
Это же решение можно представить иначе:
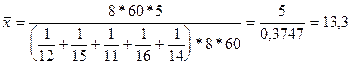
Таким образом, формула для расчета средней гармонической простой будет иметь вид:
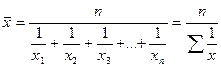
Пример 7.
Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:
| Номер завода | Издержки производства, тыс.руб. | Себестоимость единицы продукции, руб. |
Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателя и исходные данные.
Издержки производства
Средняя себестоимость = ----------------------------------------
единицы продукции ( 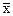 ) Количество продукции
) Количество продукции
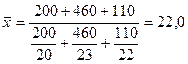 руб.
руб.
Таким образом, формулу для расчета средней гармонической взвешенной можно представить в общем виде:
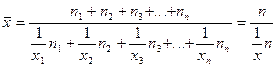
Дата добавления: 2016-11-28; просмотров: 634;
