Структурные средние
Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Пример 8.
Распределение проданной обуви по размерам характеризуется следующими показателями:
| размер обуви | и выше | ||||||||||||||||
| число пар, в % к итогу | — | — | |||||||||||||||
В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей.
Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
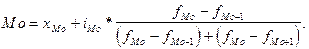
где 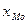 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;
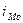 - величина модального интервала;
- величина модального интервала;
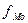 - частота модального интервала;
- частота модального интервала;
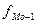 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
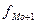 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Пример 9.
Распределение предприятий по численности промышленно - производственного персонала характеризуется следующими данными:
| Группы предприятий по числу работающих, чел | Число предприятий |
| 100 — 200 | |
| 200 — 300 | |
| 300 — 400 | |
| 400 — 500 | |
| 500 — 600 | |
| 600 — 700 | |
| 700 — 800 | |
| ИТОГО |
В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения.
Введем следующие обозначения:
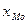 =400,
=400, 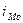 =100,
=100, 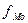 =30,
=30, 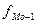 =7,
=7, 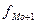 =19
=19
Подставим эти значения в формулу моды и произведем вычисления:
|
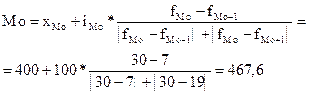
Медиана - это варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).
Например, стаж пяти рабочих составил 2, 4, 7, 8, 10 лет. В таком упорядоченном ряду медиана - 7 лет. По обе стороны от нее находится одинаковое число рабочих.
Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Пусть теперь будет не пять человек в бригаде, а шесть, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 6 и 7. Средняя арифметическая из этих значений и будет медианой ряда:
Ме = (6 + 7) / 2 = 6,5 лет.
Рассмотрим пример расчета медианы в дискретном ряду.
Пример 10.
Определим медиану заработной платы рабочих.
| Недельная з/п , руб. | Число рабочих | Сумма накопленных частот |
| 8 (2+6) | ||
| 24 (8+16) | ||
| — | ||
| — | ||
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составила ее половина - 20.
Накопленная сумма частот ряда получилась равной Варианта, соответствующая этой сумме, т.е. 160 руб., и есть медиана ряда.
Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Пример 11.
Таблица 5.8.
| Недельная з/п, руб. | Число рабочих | Сумма накопительных частот |
| 8 (2+6) | ||
| 20 (8+12) | ||
| — | ||
| — | ||
Медиана будет равна:
Ме = (150 + 170) / 2 = 160 руб.
Рассмотрим расчет медианы в интервальном вариационном ряду.
Медиана интервального вариационного ряда распределения определяется по формуле
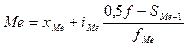
где 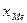 — начальное значение интервала, содержащего медиану;
— начальное значение интервала, содержащего медиану;
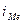 — величина медианного интервала;
— величина медианного интервала;
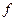 — сумма частот ряда;
— сумма частот ряда;
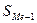 — сумма накопленных частот, предшествующих медианному интервалу;
— сумма накопленных частот, предшествующих медианному интервалу;
 — частота медианного интервала.
— частота медианного интервала.
Пример 12.
| Группы предприятий по числу рабочих | Число предприятий | Сумма накопительных частот |
| 100 — 200 | ||
| 200 — 300 | 4 (1+3) | |
| 300 — 400 | 11 (4+7) | |
| 400 — 500 | 41 (11+30) | |
| 500 — 600 | — | |
| 600 — 700 | — | |
| 700 — 800 | — | |
| ИТОГО |
Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (41), соответствует интервалу 400 - 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.
Известно, что:
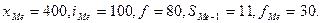
Следовательно,
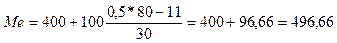 .
.
Дата добавления: 2016-11-28; просмотров: 959;
