Де V – швидкість ракети після витікання газів.
Імпульс тіла
Імпульс (кількість руху) тіла – векторна фізична величина, яка дорівнює добутку маси тіла на його швидкість
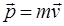 . (1.2.5)
. (1.2.5)
Імпульстіла є являється адитивною величиною. Напрямок вектора імпульсу збігається з напрямком вектора швидкості. Одиниця виміруімпульсу - кг۰м/с.
Закон збереження імпульсу.
Геометрична сума імпульсів тіл, що складають замкнуту систему, залишається постійною при будь-яких взаємодіях тіл цієї системи між собою
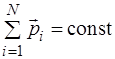 (1.2.8)
(1.2.8)
або 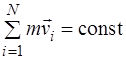 (1.2.9)
(1.2.9)
де N - число матеріальних точок (або тіл), що входять до системи.
Замкнута система - система тіл, для якої рівнодіюча зовнішніх сил дорівнює нулю.
Закон збереження імпульсу є наслідком однорідности простору: при паралельному перенесенні у просторі замкнутої системи тіл як цілого її фізичні властивості не змінюються (не залежать від вибору положення початку координат інерціальної системи відліку).
Можна доказати, що із закону збереження імпульсу виводяться три закони Ньютона.
Так, рівняння руху матеріальної точки може бути представлено у вигляді
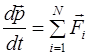 (1.2.6)
(1.2.6)
або 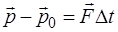 , (1.2.7)
, (1.2.7)
де 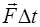 – імпульс сили, тобто добуток сили на час її дії.
– імпульс сили, тобто добуток сили на час її дії.
Зміна кількості руху пропорційна прикладеній рушійній силі і відбувається по напрямку тієї прямої, по якій ця сила діє.
На дії закону збереження імпульсу заснований реактивний рух. У ракеті при згорянні палива гази, нагріті до високої температури, викидаються з сопла з великою швидкістю 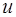 щодо ракети. Позначимо масу викинутих газів через m, а масу ракети після витікання газів через M. Тоді для замкнутої системи «ракета + гази» на підставі закону збереження імпульсу можна записати
щодо ракети. Позначимо масу викинутих газів через m, а масу ракети після витікання газів через M. Тоді для замкнутої системи «ракета + гази» на підставі закону збереження імпульсу можна записати
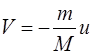 , (1.2.10)
, (1.2.10)
де V – швидкість ракети після витікання газів.
У даному випадку передбачається, що початкова швидкість ракети дорівнювала нулю. Отримана формула для швидкості ракети справедлива лише за умови, що вся маса згорілого палива викидається з ракети одночасно. Насправді витікання відбувається поступово протягом всього часу прискореного руху ракети. Кожна наступна порція газу викидається з ракети, яка вже придбала деяку швидкість.
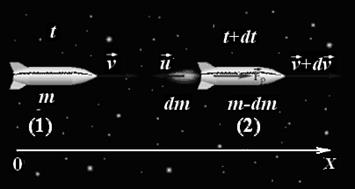
Рис. 1.2.2.Реактивний рух
Для отримання точної формули процес закінчення газу з сопла ракети потрібно розглянути більш детально. Нехай ракета в момент часу t має масу m і рухається зі швидкістю 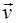 (рис. 1.2.2).
(рис. 1.2.2).
Протягом малого проміжку часу dt з ракети буде викинута деяка порція газу з відносною швидкістю 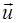 Ракета в момент t+dt буде мати швидкість
Ракета в момент t+dt буде мати швидкість 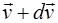 , а її маса стане рівною m+dm, де dm<0. Маса викинутих газів буде, очевидно, дорівнювати –dm > 0. Швидкість газів в інерціальній системі OX дорівнюватиме
, а її маса стане рівною m+dm, де dm<0. Маса викинутих газів буде, очевидно, дорівнювати –dm > 0. Швидкість газів в інерціальній системі OX дорівнюватиме 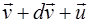 . Застосуємо закон збереження імпульсу. У момент часу t+dt імпульс ракети дорівнює
. Застосуємо закон збереження імпульсу. У момент часу t+dt імпульс ракети дорівнює 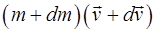 , а імпульс газів, що випускаються, дорівнює
, а імпульс газів, що випускаються, дорівнює 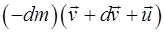 . У момент часу t імпульс всієї системи дорівнював
. У момент часу t імпульс всієї системи дорівнював  . Припускаючи, що система «ракета + гази» замкнена, можна записати:
. Припускаючи, що система «ракета + гази» замкнена, можна записати:
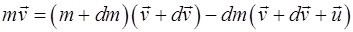 . (1.2.11)
. (1.2.11)
Дата добавления: 2016-11-28; просмотров: 1031;
