График функции. Построение графика обратной функции

Определение 11.5.

Графиком функции y=f(x) называется множество точек плоскости, координаты которых соответствуют аналитическому выражению y=f(x).

Для построения графика обратной функции вспомним, что мы рассматриваем зависимость x от y. Поэтому то, что было областью определения для исходной (прямой) функции станет множеством значений обратной и наоборот. Поэтому график обратной функции будет отражением графика исходной относительно оси y = x. Очевидно, что в обратной функции сохраняется порядок возрастания-убывания исходной функции, поэтому, если исходная функция возрастала или убывала, обратная функция будет таковой же.(см.рис.11.5)

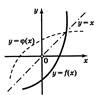
Рис.11.5

Рассмотрим построение графика обратной функции на примере функции y = sin x.

График прямой функции имеет вид:

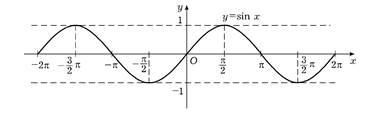
где бесконечному количеству различных х соответствует в силу периодичности одно и то же значение y. Рассмотрим отрезок [-π/2, π/2], на котором функция инъективна и является возрастающей, а ее значения меняются на промежутке [-1,1] и сужение функции y = sin x на этот промежуток.

Соответственно, областью определения обратной функции станет промежуток [-1,1], а множеством значений – промежуток [-π/2, π/2].

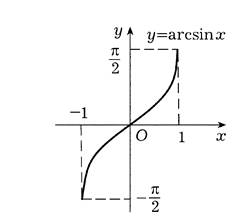
Принимая во внимание симметрию относительно оси y=x и возрастание прямой функции, получим график обратной функции y=arcsin x :