Способы задания функции

Понятие функции. График функции.

Важнейшие разделы современной математики сосредоточиваются вокруг понятий функции и предела.

Такие выражения, как, например, x² + 2x − 3, не имеют определенного числового значения, пока не указано значение x.

Говорят, что значение этого выражения есть функция значения x, и пишут

x² + 2x − 3 = f(x).

Например, если x = 2, то 2² + 2 · 2 − 3 = 5, так что f(2) = 5. Таким же образом непосредственной подстановкой можно найти значение функции f(x) при любом целом, дробном, иррациональном и даже комплексном значении x.

Количество простых чисел, меньших чем n, есть функция π(n) целого числа n. Когда задано значение числа n, то значение функции π(n) определено, несмотря на то что неизвестно никакого алгебраического выражения для его подсчета. Площадь треугольника есть функция длин трех его сторон; она меняется вместе с ними и делается фиксированной, если зафиксированы длины сторон. Если плоскость подвергается проективному или топологическому преобразованию, то координаты точки после преобразования зависят от первоначальных координат точки, т. е. являются их функциями. Понятие «функция» выступает каждый раз, как только величины связаны каким-нибудь определенным физическим соотношением. Объем газа, заключенного в цилиндр, есть функция температуры и давления, оказываемого на поршень. Замечено,

что давление атмосферы на воздушный шар есть функция высоты шара над уровнем моря. Целая область периодических явлений — движение приливов, колебание натянутой струны, распространение световых волн, испускаемых накаленной проволокой, — «регулируется» простыми тригонометрическими функциями sin x и cos x.

Для самого Лейбница (1646–1716), который впервые ввел термин «функция», и для математиков XVIII в. идея функциональной зависимости более или менее идентифицировалась с существованием простой математической формулы, точно выражающей эту зависимость.

Такая концепция оказалась слишком узкой по отношению к требованиям, предъявленным математической физикой, и понятие «функция» вместе с упомянутым выше понятием «предел» впоследствии длительно подвергалось обобщениям и шлифовке.

Определение 11.1.

Функция –это отображение множества X в множество YX→Y, где множество Y – числовое.

X называется область (множеством) определения функции , Y – множество ее значений

Если каждому значению x какого-либо промежутка на основании некоторого правила приводится в соответствие определенное значение y, то говорят: y является функцией от x и пишут символически

y=f(x), y=F(x) y=g(x)

или как-нибудь аналогично . При этом x называют независимой, y – зависимой величиной (переменной), x называют также аргументом функции.

В общем определении понятия заданной в некотором интервале функции ничего не говорится о характере того правила, согласно которому зависимая переменная получается из независимой. Это правило может быть как угодно сложно, и в некоторых теоретических вопросах эта общность является преимуществом. Однако в большинстве случаев , в частности, в дифференциальном и интегральном исчислении и в приложениях, функции, с которыми приходится иметь дело, не обладают наибольшей общностью; напротив, законы соответствия, относящие каждому значению x определенное значение y, в каждом вопросе обычно подчиняют некоторым упрощающим ограничениям.

Понятие функциональной зависимости имеет исключительное значение не только в самой «чистой» математике, но также и в практических ее приложениях. Физические законы являются не чем иным, как выражением способа, посредством которого некоторые величины зависят от других, способных изменяться так или иначе. Так, например, высота

звука, производимого колеблющейся струной, зависит от ее длины, от ее веса и от степени ее натяжения; давление атмосферы зависит от высоты; энергия пули зависит от ее массы и скорости. Задача физики состоит в точном или приближенном определении природы всех подобного рода зависимостей.

С помощью понятия функции можно дать точную в математическом смысле характеристику движения. Если представим себе, что движущаяся частица сосредоточена в некоторой точке пространства с прямоугольными координатами x, y, z, и если переменное t измеряет время, то движение частицы полностью определено заданием координат x, y, z как функций времени:

x = f(t), y = g(t), z = h(t).

Примером этого может служить свободное падение частицы по вертикали под действием одной лишь силы тяжести: мы имеем в этом случае соотношения

x = 0, y = 0, z = − ½ gt²

где g обозначает ускорение силы тяжести. Если частица равномерно вращается по единичной окружности в плоскости x, y, то движение ее характеризуется функциями

x = cos wt, y = sin wt,

где w—постоянное число (так называемая угловая скорость вращения).

Замечание 11 (1).

Под математической функцией следует понимать просто закон, управляющий взаимными зависимостями переменных величин — и не более того. Понятие функции не подразумевает существования чего-либо близкого к «причине и следствию» в отношениях между независимой и зависимой переменными. Хотя в обыденной речи термин «функциональная зависимость» сплошь и рядом употребляется именно в этом последнем смысле, мы будем избегать такого рода философских интерпретаций. Так, например, закон Бойля, относящийся к газу, заключенному в некоторую замкнутую оболочку при постоянной температуре, утверждает, что произведение давления газа p на его объем v есть величина постоянная, равная c (последнее значение, в свою очередь, зависит от температуры):

pv = c.

Это соотношение можно решить как относительно p, так и относительно v:

p = c/v или v = c/p ;

при этом не следует подразумевать ни того, что перемена объема есть «причина» изменения давления, ни того, что изменение давления есть «причина» изменения объема. Для математика существенна лишь форма соответствия (связи) между двумя переменными величинами, которые он рассматривает.

Замечание 11.1. (2) (Курант, Роббинс «Что такое математика?»)

Следует заметить, что подход к понятию функции несколько отличается у математиков и у физиков. Математики обычно подчеркивают закон соответствия, математическую операцию, которую нужно применить к значению независимого переменного x, чтобы получить значение зависимого переменного u. В этом смысле f( ) есть символ математической операции; значение u = f(x) есть результат применения операции f( ) к числу x. С другой стороны, физик часто более заинтересован в самой величине u как таковой, чем в какой-то математической процедуре, с помощью которой значение u может быть получено из значения x. Так, например, сопротивление u воздуха движению предмета зависит от скорости v движения и может быть найдено экспериментальным путем, независимо от того, известна ли явная математическая формула для вычисления u. Физика прежде всего интересует фактическое сопротивление, а не специальная математическая формула f(v), если только эта формула не помогает при анализе поведения величины u. Таково обычно отношение тех, кто применяет математику к физике или инженерному делу.

В некоторых высших разделах математического анализа, чтобы избежать путаницы, иногда бывает существенно различать совершенно отчетливо, будет ли под символом u = f(x) подразумеваться операция f( ), применяемая к x для получения u, или же сама величина u, которая, в свою очередь, может рассматриваться как зависимая, и совсем другим образом, от некоторой другой переменной z. Например, площадь круга задается функцией u = f(x) = πx², где x — радиус круга, но можно также написать: u = g(z) = z² / 4π , понимая под z

длину окружности.

Способы задания функции

Всякий закон природы, дающий связь одних явлений с другими, устанавливает функциональную зависимость между величинами.

Существует много способов для изображения функциональных зависимостей, но самое важное значение имеют три способа:

1) аналитический,

2) способ таблиц и

3) графический, или геометрический.

Мы говорим, что функциональная зависимость между величинами или, проще, функция изображена аналитически, если величины эти связаны между собой уравнениями, в которые они входят, подвергаясь различным математическим операциям: сложению, вычитанию, делению, логарифмированию и т. д. К аналитическому изображению

функций мы приходим, когда исследуем вопрос теоретически, т. е., установив основные предпосылки, мы применяем математический анализ и получаем результат в виде некоторой математической формулы.

Если мы имеем непосредственное выражение функции (т. е. зависимой переменной) при помощи математических действий над другими, независимыми переменными, то говорят, что функция аналитически задана явно. Примером явного задания функции может служить выражение объема газа v при постоянной температуре через давление (явная функция одной независимой переменной):

или выражение площади треугольника S через три его стороны (формула Герона)

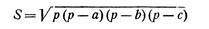- явная функция трех независимых переменных

Рассмотрим таблицу включающую значения высоты над уровнем моря h и среднегодовую температуру t и устанавливающая зависимость между этими переменными

Такой способ задания называется табличным

Зная аналитическое задание функции можно составить таблицу ее значений. Так например для функции y = x соответствующая таблица будет иметь вид:

Возникает вопрос: всегда ли можно о табличного задания функции перейти к ее аналитическому выражению, т.е. записать такую функцию формулой?

Для этого заметим, что таблица дает не все значения функции, причем промежуточные значения функции могут быть найдены лишь приближенно ( так называемое интерполирование функции). Поэтому в обще случае точное аналитическое выражение функции по ее табличным данным нельзя. Однако всегда можно построить формулу, и притом не одну, которая для значений аргумента, имеющихся в таблицу, будет давать соответствующие табличные значения функции. Такого рода формулы носят название интерполяционных.

Аналитический и табличный способы изображения функции «страдают» отсутствием наглядности. Этого недостатка лишен графический способ задания функции y=f(x), когда соответствие между аргументом x и функцией y=f(x) устанавливается с помощью графика

(см. рис.11.2)

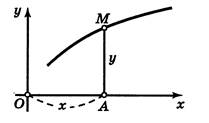
Рис.11.2

Здесь чтобы для некоторого значения аргумента, например х, найти отвечающее ему значение y функции, нужно на оси Ox отложить в соответствующем направлении отрезок OA=x, а затем построить перпендикуляр AM до пересечения с графиком. Взяв длину этого перпендикуляра с надлежащим знаком, мы и получим число y=f(x). Давая х различные значения, мы с помощью этого приема будем иметь соответствующие значения y, которые, если это нужно, можно записать в виде таблицы.

Сложная функция

Часто приходится рассматривать такую функцию y=f(x), аргумент которой сам является функцией вида x = g(t) некоторой новой переменой t. В таком случае говорят, что переменная y представляет собой сложную функцию аргумента t, а переменную x называют промежуточным аргументом. Указанную функцию называют также суперпозицией функций f и g и обозначают y = f[g(t)] или y = f ◦g.

Очевидно, что значения функции g не должны покидать пределы области определения функции f. Например, полагая z =log y, y=sin x, мы можем рассматривать лишь такие x , для которых sin x>0, иначе выражение log sin x не имело бы смысла

Стоит заметить, что характеристика функции как сложной связана не с природой функциональной зависимости z от х, а лишь со способом задания этой зависимости.

Например, пусть

Здесь функция cos x оказалась заданной в виде сложной функции

Пример 11.3. (1).

Проиллюстрируем возникновение понятия сложной функции. Предположим, что материальная точка М равномерно и с постоянной угловой скоростью ω вращается по окружности радиуса R.

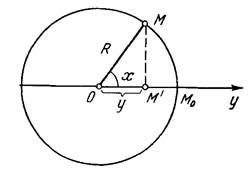Рис. 11.3

Найдем закон движения проекции М’ точки М на некоторую (горизонтальную) ось Oy , проходящую через центр О окружности и лежащую в ее плоскости (см рис. 11.3.). Предположим, что в начальный момент времени t=0 движущаяся точка М находится в точке М₀ пересечения окружности с осью Oy . Обозначим через y координату проекции М’ точки М на ось Oy, а через x – угол М₀ОМ, на который повернется точка М за время t. Очевидно, что y = R cosx, где x = ωt. Тогда координата y проекции М’ представляет собой сложную функцию времени t вида y = R cosx, где x = ωt. Эту сложную функцию можно записать в виде y = R cos ωt.

Движение по закону y = R cos ωt в механике называется гармоническим колебанием.

Пример 11.3(2)

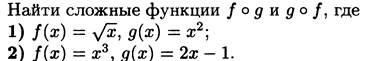
Решение:

1)По определению композиции функций имеем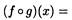

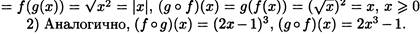
Обратная функция.

Пусть y есть функция аргумента x: y=f(x). Задавая значения х, будем получать соответствующие значения y. Можно, однако, считая аргументом y и вычислять соответствующие значения х. В таком случае данное уравнение будет определять х как функцию от y :

,

где функция 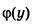для всех допустимых значений y

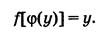
Иногда придерживаются стандартных обозначений: под х понимают независимую переменную, под y – функцию, то есть зависимую переменную. В таком случае обратную функцию следует писать в виде

Вспомним, что нами было показано, что для построения обратного отображения (в данном случае функции) необходимо и достаточно, чтобы исходное отображение было биективным. В случае, если разным значениям переменной х может соответствовать одно и то же значение y (как, например, в тригонометрических функциях), рассматривается сужение функции на промежуток, на котором разным х соответствуют разные y.

Очевидно, что функция, обратная к функции есть функция y = f(x).. Поэтому функции с характеристиками f и φ, связанные отношением

, являются взаимно обратными. Одна из них называется прямой, другая – обратной. Одна та же кривая y = f(x) представляет собой график данной функции и график обратной ей функции, смотря по тому, на какой из осей ox или oy, откладываются значения аргумента.

Пример 11.4

Построить функцию, обратную данной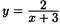

Функция убывает на всей области определения (х – любое действительное число≠ -3), поэтому у нее есть обратная, которую можно найти, разрешая исходное уравнение относительно х (выражаем х через y и меняем местами х и y). Искомая обратная функция: