Строение электронных оболочек

Сведения о строении электронных оболочек накапливались и развивались с конца XIX до середины ХХ века. Для строгого описания движении электронов вокруг атомного ядра необходимо использовать понятие корпускулярно-волнового дуализма электрона (электрон обладает одновременно свойствами частицы и волны).

Количественно волновой дуализм электрона и других элементарных частиц описывается уравнением Луи де Бройля:

,

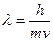где l – длина волны частицы;

m – масса частицы;

v – скорость ее движения;

h – постоянная Планка (h = 6,62×10^-34 Дж×с).

 

Микрочастицы подчиняются принципу неопределенности Гейзенберга – для микрочастиц невозможно одновременно определить координату (х) и составляющую импульса (р) вдоль этой координаты: Dх × Dр_х ³ h

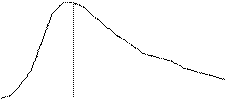
В связи с этим, для описания поведения микрочастиц вводят особую функцию, которую называют функцией состояния или волновой функцией, Y. Она вводится таким образом, что квадрат ее модуля пропорционален вероятности обнаружить частицу (электрон) в данной точке в указанное время (плотность вероятности). Функция плотности вероятности достигает максимального значения на некотором конечном расстоянии от ядра. Например, для электрона атома водорода функция плотности вероятности имеет следующее распределение по всем осям координат:

 

½Y²½

 

 

r₀ r

 

Волновая функция электрона носит название «орбиталь». Она характеризует энергию и форму пространственного распределения электронного облака.

 

Количественные соотношения в теории строения атома определяются волновым уравнением Шредингера:

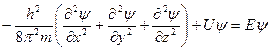, где

U – потенциальная энергия электрона;

Е – полная энергия электрона;

m – масса электрона;

x, y, z – координата электрона;

y – волновая функция;

 

Решение уравнения Шредингера содержит набор квантовых чисел, характеризующих поведение электрона в атоме.

n – главное квантовое число, оно определяет общий запас энергии электрона, т.е. энергетический уровень.

n = 1,2,3…

l – орбитальное квантовое число, определяет форму электронной орбитали (энергетический подуровень).

l = 0,1,2…(n-1).

Если l = 0, то орбиталь называется s-орбиталь (движение электрона по сфере). При l = 1 мы имеем р-орбиталь (гантелевидная форма движения). Формы движения электронов по d- и f- орбиталям (l = 2 и 3 соответственно) имеют еще более сложный вид.

Число подуровней на энергетическом уровне совпадает с его номером. Так, для первого уровня (n = 1) существует только один подуровень (l = 0), то есть 1s-орбиталь. Аналогично для n = 2 (второй уровень) имеем два подуровня (l = 0, 1) или 2s,2p-орбитали; для третьего уровня (n = 3, l = 0, 1, 2) – 3s,3p,3d-орбитали и т.д.

m_l – магнитное квантовое число, характеризует проекцию магнитного момента электрона на внешнее магнитное поле, то есть определяет ориентацию электронной орбитали в пространстве. Его значения определяются орбитальным квантовым числом: m_l = ±l; ±(l-1); ±(l-2)…0.

При значении орбитального квантового числа l = 0 магнитное квантовое число имеет одно возможное значение (m_l = 0), то есть возможен только один способ ориентации s-орбитали в пространстве. Аналогично получаем, что для р-орбиталей (l = 1, m_l = –1, 0, +1) существуют три возможных способа ориентации (вдоль осей координат), для d-орбиталей – пять возможных способов ориентации (l = 2, m_l = –2, –1, 0, +1, +2) и т.д.

На основе представлений о квантовых числах можно уточнить понятие электронной орбитали. Атомная орбиталь – это совокупность положений электрона в атоме, характеризуемых определенными значениями главного, орбитального и магнитного квантовых чисел. Условно атомные орбитали обозначают в виде клетки (энергетической ячейки):

m_s – спиновое квантовое число, определяет собственный момент вращения электрона. Это квантовое число вытекает не из решения уравнения Шредингера, а из анализа атомных спектров. Магнитное квантовое число может принимать два значения:

m_s = ± ½.

Условно электроны, имеющие разные значения спинового квантового числа, обозначаются противоположно направленными стрелками: ­¯ .