Застосування трансверсальних фільтрів та еквалайзера зі зворотнім зв’язком для подавлення шумів квантування та інтерференції
 Навіть при передачі одиничного однополярного імпульсу в каналі зв’язку одержують спотворення сигналу у вигляді основного дзвоноподібного імпульсу, який супроводжується шумовими коливаннями більш високих частот. Тому система із додатковим квантуванням вхідних сигналів, якими є цифрові СПД, використовує схеми додаткового формування сигналів у вигляді активних фільтрів. Це можуть бути так звані еквалайзери, трансверсальні фільтри, косинусні коректори, схеми із перехресним зв’язком та ін.
Навіть при передачі одиничного однополярного імпульсу в каналі зв’язку одержують спотворення сигналу у вигляді основного дзвоноподібного імпульсу, який супроводжується шумовими коливаннями більш високих частот. Тому система із додатковим квантуванням вхідних сигналів, якими є цифрові СПД, використовує схеми додаткового формування сигналів у вигляді активних фільтрів. Це можуть бути так звані еквалайзери, трансверсальні фільтри, косинусні коректори, схеми із перехресним зв’язком та ін.
Найбільш вживаними є трансверсальні фільтри, що складаються з ряду елементів затримки і компараторів із заданими правовими коефіцієнтами.
Трансверсальні фільтри складаються з ліній затримки та окремих секцій із заданими ваговими коефіцієнтами. В результаті вихідний сигнал формується як сума зважених значень гармонік прийнятого сигналу. теоретично можна реалізувати безмежну розмірну секцію з різними ваговими коефіцієнтами гармонік. Окремі вагові коефіцієнти {Cn} вибираються таким чином, щоб рахувати ефекти інтерференції символів, що є сусідніми в часовому просторі.
Нехай вибрано 2N+1 відвід від секції лінії затримки з відповідними ваговими коефіцієнтами C-N, C-N+1, …, C0, C1, …, CN. Вибірки на виводі трансверсального фільтра знаходяться шляхом згортки вибірок на входах {x(k)} та з врахуванням вагових коефіцієнтів CN. Значення {z(k)} описується співвідношенням:

Структурна схема фільтра повинна містити також додатковий вузол алгоритмізації – корекції вагових коефіцієнтів.

Аргумент k є фізичним часовим коефіцієнтом, що може приймати значення як від’ємні, так і додатні. Коефіцієнт n використовується для позначення зміщення в часі і як ідентифікатор коефіцієнта фільтра. Якщо ввести вектор Z:
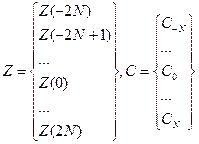
Тоді матриця Х буде мати значення:
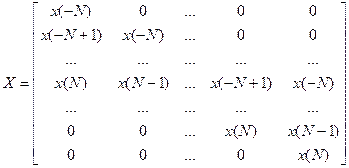
Отже, отримується співвідношення:  - зв'язок між набором вхідних сигналів Х, вихідних сигналів Z і вагових коефіцієнтів С.
- зв'язок між набором вхідних сигналів Х, вихідних сигналів Z і вагових коефіцієнтів С.
В загальному випадку розміри вектора Z можуть бути довільними, так само як і число матриці Х. це зумовлене тільки вимогами до умов міжсимвольної інтерференції в точках вибірок даних.
При записі системи рівнянь у векторній формі можна одержати перевизначену систему, коли кількість рівнянь є значно більша, ніж кількість невідомих. Це свідчить про надлишковість матричних елементів. На практиці використовують три відвідні та семи відвідні еквалайзери, які забезпечують мінімізацію вкладу між символьної інтерференції в основний сигнал на рівні 0,0095, що не перевищує 1 %.
 В еквалайзерах із зворотним зв’язком за методикою прийняття рішень використовується додатково прямий фільтр та фільтр зворотного зв’язку. Це дозволяє підвищити продуктивність обробки сигналів в каналах з переважаючими нульовими значеннями спектральних складових. Структурно такий еквалайзер відображається наступною схемою:
В еквалайзерах із зворотним зв’язком за методикою прийняття рішень використовується додатково прямий фільтр та фільтр зворотного зв’язку. Це дозволяє підвищити продуктивність обробки сигналів в каналах з переважаючими нульовими значеннями спектральних складових. Структурно такий еквалайзер відображається наступною схемою:
В якості прямого та зворотного фільтрів можуть використовуватись лінійні фільтри, зокрема трансверсальні. Нелінійність фільтру із зворотним зв’язком може бути обумовлена не лінійністю характеристики детектора. Суть роботи такого еквалайзера наступна:
Якщо значення одержаних попередньо символів відомі, то між символьну інтерференцію, одержану за рахунок їх взаємодії, можна точно врівноважити на виході прямого фільтру шляхом віднімання значення попередніх символів з відповідними ваговими коефіцієнтами.
Для забезпечення задовільних значень вибраного критерію, наприклад, середньоквадратичної похибки, вагові коефіцієнти для прямого і зворотного фільтрів можуть коректуватися одночасно. При використанні тільки прямого фільтру, на виході присутній шум квантування, зумовлений дискретизацією вибірок сигналів.
Перевагою реалізації DFE-фільтра є те, що фільтр зворотного зв’язку використовується не тільки для видалення між символьної інтерференції, але і працює без шумів квантування, що забезпечує відмінність шуму каналу обробки на цифровому виході.
Дата добавления: 2016-11-02; просмотров: 1105;
