Построение графиков.
Основная команда для построения графиков функций одной переменной в MATLAB – команда plot. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах (Figure).
Возьмем вначале простейший пример – построим график синусоиды. Следует помнить, что MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между соседними точками. Зададим интервал изменения аргумента х от 0 до 10 с шагом 0.1.
Текст соответствующего M-файла:
| x=0:0.1:10; y=sin(x); plot(x,y) |
Графическое окно с результатом представлено на рис. 1.
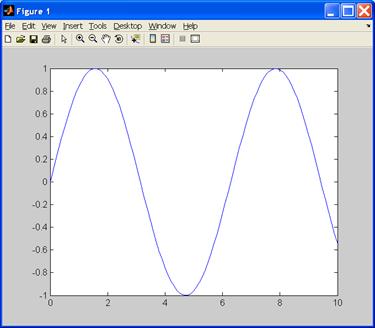
Рис. 1. Графическое окно, в котором построен график синусоиды.
Дополнительные возможности для оформления графиков:
· hold on (hold off) – объединение (отключение) нескольких графиков на одних координатных осях;
· grid on (grid off) – нанесение (отключение) линий сетки на график;
· title(‘заголовок’) – вывод заголовка функции;
· xlabel(‘подпись под осью x’),ylabel(‘подпись под осью y’) – соответственно подписи осей х и у;
· text(m,n,’надпись’)– надпись в заданном месте рисунка, m и n – координаты точки на графике, начиная с которой выводится запись (координаты точки задаются в тех же единицах измерения, что и координаты осей графика);
· legend(‘легенда 1’, ‘легенда 2’, … , ‘легенда n’, k)– легенды для каждого из n-графиков k – местоположение легенды.
· Функцияsubplot(m,n,p) – это разделение графического окна MATLAB на несколько подокон с различными графиками, где m и n – число частей по вертикали и по горизонтали, на которые делится графическое окно, p – номер подокна в котором нужно отобразить график.
Полная форма команды построения графиков функций одной переменной:
plot(x1,y1,s1,x2,y2,s2, … ,xn,yn,sn)
где x1, x2, … , xn – массивы абсцисс графиков; y1, y2, …, yn – массивы ординат; s1, s2, … , sn – строка, состоящая из трех символов, которые определяют цвет линии, тип маркера и тип линии графиков.
Кроме того, для построения графиков функций одной переменной можно использовать графическую функцию fplot. Она позволяет строить график функции, заданной в символьном виде (например, арифметическое выражение, определяющее функцию, заключено в апострофы), в интервале изменения аргумента 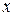 от xmin до xmax без фиксированного шага изменения х. Рассмотрим ее применение для построения графика функции
от xmin до xmax без фиксированного шага изменения х. Рассмотрим ее применение для построения графика функции 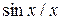 на интервале от -10 до 10. Эта функция имеет устранимую неопределенность в точке 0. Построение ее графика с помощью plot в этой точке не представляется возможным. Соответствующее графическое окно с графиком представлено на рис. 2. Заметим, что в точке
на интервале от -10 до 10. Эта функция имеет устранимую неопределенность в точке 0. Построение ее графика с помощью plot в этой точке не представляется возможным. Соответствующее графическое окно с графиком представлено на рис. 2. Заметим, что в точке 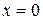 результат правильный, т.е.
результат правильный, т.е.  .
.
Текст соответствующего M-файла:
| fplot('sin(x)/x',[-10,10]);grid on |

Рис. 2. Графическое окно, в котором построен график sin(x)/x.
Команда grid on (сетка) позволяет включить отображение сетки, которая строится пунктирными линиями.
Таблица 1.6. Параметры для управления цветом и видом графиков.
| Параметр | Обозначение |
| Тип линии | |
| сплошная | - |
| пунктирная | : |
| штриховая | -- |
| штрихпунктирная | -. |
| Цвет линии | |
| красный | r |
| желтый | y |
| зеленый | g |
| синий | b |
| голубой | c |
| розовый | m |
| черный | k |
| белый | w |
| Тип маркера | |
| точка | . |
| кружок | о |
| крестик | x |
| плюс | + |
| звездочка | * |
| квадрат | s |
| ромб | d |
| треугольник вершиной вниз | v |
| треугольник вершиной вверх | ^ |
Пример. Построение графика функции на отрезке [-5; 5] , используя графические функции plot и fplot
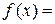

Пример текста программы для М-файла
x=-5:0.5:5;
y=x.^4+4*x.^3-6*x.^2+12*x-1;
hold on
fplot('x^4+4*x^3-6*x^2+12*x-1',[-5,5],'c')
plot(x,y,'-.m*')
grid on

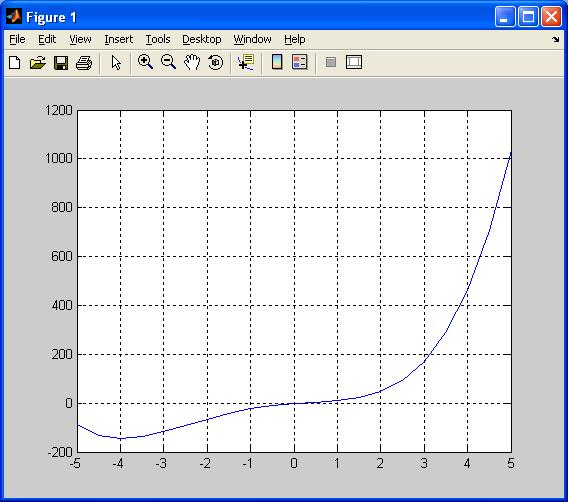
Примеp. Определение наибольшего и наименьшего значения функции на отрезке [-5; 5] и построение ее графика
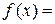

Пример текста программы для М-файла
x=-5:0.5:5;
y=x.^4+4*x.^3-6*x.^2+12*x-1;
plot(x,y)
grid on
[ymin,imin]=min(y);
disp('xmin='),disp(x(imin)),disp('fmin=f(xmin)='),disp(ymin)
[ymax,imax]=max(y);
disp('xmax='),disp(x(imax)),disp('fmax=f(xmax)='),disp(ymax)
Результат счета
xmin=
-4
fmin=f(xmin)=
-145
xmax=
fmax=f(xmax)=
Дата добавления: 2016-11-02; просмотров: 2259;
