Плоское движение твердого тела
Движение твердого тела называется плоским(плоскопараллельным), если каждая точка тела движется в одной и той же плоскости.
8.1.1 Свойства плоского движения:
ü 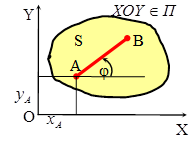 точки тела движутся в плоскостях параллельных между собой и некоторой фиксированной плоскости П0;
точки тела движутся в плоскостях параллельных между собой и некоторой фиксированной плоскости П0;
ü траектории точек – плоские кривые;
ü для изучения плоского движения тела достаточно изучить движение плоской фигуры S в сечении плоскостью П÷÷ П0;
ü 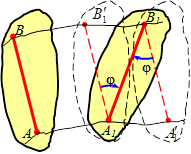 положение плоской фигуры S однозначно определяется положением в этом сечении отрезка АВ; положение отрезка АВ однозначно определяется координатами произвольно выбранной точки А (полюса) и углом φ:
положение плоской фигуры S однозначно определяется положением в этом сечении отрезка АВ; положение отрезка АВ однозначно определяется координатами произвольно выбранной точки А (полюса) и углом φ: 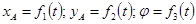 - уравнения плоского движения твердого тела;
- уравнения плоского движения твердого тела;
ü движение плоской фигуры S в ее плоскости П может рассматриваться как сумма поступательного движения всех точек фигуры, движущихся как полюс – точка А и вращения фигуры S вокруг этого полюса;
ü поступательное движение полюса и угол поворота φ не зависят от выбора полюса.
 8.1.2 Теорема сложения скоростей плоской фигуры:
8.1.2 Теорема сложения скоростей плоской фигуры:
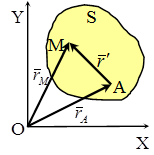
Теорема: Скорость любой точки (М) плоской фигуры геометрически складывается из скорости какой-либо другой точки (А), принятой за полюс и скорости, которую данная точка (М) получит при вращении фигуры вокруг полюса.
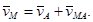
Доказательство
Так как 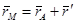 , то
, то
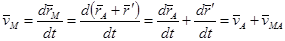 .
.
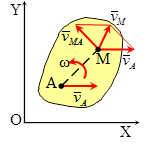 Вектор
Вектор 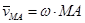 и направлен перпендикулярно АМ в сторону указанную угловой скоростью ω. Модуль и направление вектора
и направлен перпендикулярно АМ в сторону указанную угловой скоростью ω. Модуль и направление вектора 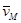 определяют по правилу параллелограмма. Векторное уравнение
определяют по правилу параллелограмма. Векторное уравнение 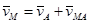 может быть решено аналитически (для этого его проецируют на оси координат) и графически (строят план скоростей, см. ниже).
может быть решено аналитически (для этого его проецируют на оси координат) и графически (строят план скоростей, см. ниже).
8.1.3 Планом скоростей называется векторная диаграмма, построенная на основе теоремы сложения скоростей. Покажем порядок построения плана скоростей для кривошипно-ползунного механизма – широко распространенного в сельхозмашиностроении и других отраслях.
Кривошипно-ползунный механизм состоит из трех подвижных звеньев: кривошипа ОА; шатуна АВС; ползуна (поршня) В и неподвижной стойки (заштриховано). Если заданы: положение механизма, угловая скорость кривошипа ωОА, длины звеньев 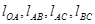 , то можно рассчитать модуль скорости точки А по формуле
, то можно рассчитать модуль скорости точки А по формуле 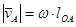 ; вектор
; вектор 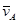 направлен перпендикулярно кривошипу ОА в сторону, указанную
направлен перпендикулярно кривошипу ОА в сторону, указанную 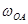 .
.
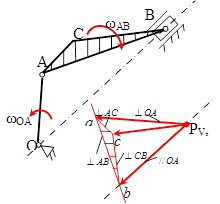 Из произвольной точки РV (полюс плана скоростей) отложим в масштабе вектор
Из произвольной точки РV (полюс плана скоростей) отложим в масштабе вектор 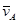 , его конец обозначим буквой а. Шатун АВ совершает плоское движение, применим к нему теорему сложения скоростей
, его конец обозначим буквой а. Шатун АВ совершает плоское движение, применим к нему теорему сложения скоростей
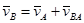 .
.
Из конца вектора 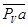 проведем перпендикуляр к АВ, а из полюса плана PV//OB. Точку пересечения обозначим b. Проведем из полюса PV стрелки к точкам a и b. Это в масштабе векторы скоростей
проведем перпендикуляр к АВ, а из полюса плана PV//OB. Точку пересечения обозначим b. Проведем из полюса PV стрелки к точкам a и b. Это в масштабе векторы скоростей 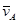 и
и 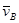 . Вектор
. Вектор 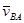 изображен на плане скоростей отрезком ab и направлен от a к b.
изображен на плане скоростей отрезком ab и направлен от a к b.
Чтобы определить скорость точки С шатуна составим по теореме сложения скоростей два векторных уравнения, приняв за полюсы точки А и В:
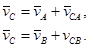
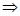
Чтобы совместно графически решить эти уравнения, проведем из точки a плана скоростей перпендикуляр к АС, а из точки b перпендикуляр к ВС. Точку их пересечения обозначим с. Стрелка из полюса плана скоростей PV к точке c – в масштабе вектор 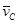 . План построен.
. План построен.
Свойства плана скоростей:
ü масштаб плана скоростей определяется по заданному вектору скорости ( 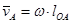 или
или 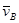 ) с помощью масштабного коэффициента
) с помощью масштабного коэффициента 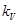 , который рассчитывают разделив модуль заданной скорости на выбранную длину, например,
, который рассчитывают разделив модуль заданной скорости на выбранную длину, например, 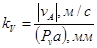 ;
;
ü полюс плана скоростей точка PV, в этой точке находятся точки, скорость которых равна нулю (например, неподвижная точка стойки О;
ü скорость любой точки механизма относительно стойки (например, 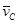 ) изображается отрезком, направленным от полюса плана PV к соответствующей точке (отрезок Pvc);
) изображается отрезком, направленным от полюса плана PV к соответствующей точке (отрезок Pvc);
ü скорость вращения одной точки какого-либо звена вокруг другой (например, точки С вокруг точки А - 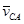 ) изображается одноименным отрезком (ac), направлен вектор к той точке, которую вращают (к точке с);
) изображается одноименным отрезком (ac), направлен вектор к той точке, которую вращают (к точке с);
ü модуль угловой скорости звена равен частному от деления скорости вращения одной точки этого звена вокруг другой на натуральную длину расстояния между точками на звене механизма (например, 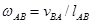 );
);
ü модуль любой скорости механизма можно определить, умножив длину соответствующего отрезка на плане скоростей на масштабный коэффициент (например, 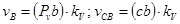 );
);
ü если на плане найдены скорости двух точек звена, то скорость любой другой точки этого звена можно найти по правилу подобия: если на звене механизма точки образуют геометрическую фигуру, то одноименные точки на плане скоростей образуют подобную сходственно расположенную (повернутую в плоскости чертежа) фигуру (например, 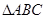 ~
~ 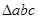 ).
).
8.1.4
Дата добавления: 2016-05-11; просмотров: 860;
