Расчет погрешностей оборудования

(методических и инструментальных)

Источники ошибок:

1. Приборные погрешности

- неправильные измерения датчика;

- неправильные показания индикатора (точность индикатора не соответствует точности датчика).

2. Методические погрешности

- ошибки наблюдателя (оператора). Делятся на субъективные (плохое настроение) и объективные (неправильный метод).

3. Случайные погрешности

- шумовые воздействия (воздействия неучтенных факторов).

Классы ошибок:

- систематические;

- случайные.

Систематические ошибки - такие ошибки, у которых среднее значение последовательных измерений отклоняются от известного точного значения в течение длительных измерений независимо от их числа. К ним относятся погрешности прибора, связанные с его конструкцией, погрешности, связанные с методом измерений.

Систематическая ошибка устраняется путем построения графика, который сравнивается с эталонным, и устраняется погрешность калибровки (δ_к). Указанная погрешность калибровки учитывается при последовательных измерениях прибора, путем прибавления или вычитания указанной погрешности.

Систематическую ошибку можно оценить с помощью калибровки прибора по известному эталону.

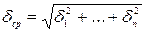
Случайные погрешности возникают при влиянии разовых случайных факторов и определяется по формуле:

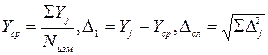
Из случайной и систематической погрешности рассчитывается истинная погрешность. Истинная и случайная погрешности подчиняются нормальному закону распределения событий.

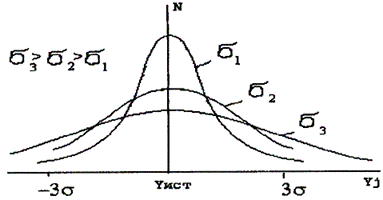
Рис.20. График систематической и случайной погрешности

,

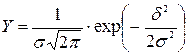где d - теоретическое отклонение или дисперсия рассеяния измерений относительно среднего Y или Y_ист;

S = d - эмпирическое отклонение, рассеяние относительно Y_ср.

Для определения вида кривой проводится совокупность измерений:

- генеральная совокупность N®¥, теоретические параметры – δ, Y_ист = M{Y_i}

- выборка N = n, теоретические параметры – S, Y_{j ср}.

M{Y_i} – математическое ожидание измерений параметра.

При N®¥ достаточно истинное значение, когда математическое ожидание M{Y} перестает изменяться (математическое истинное значение).

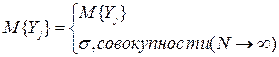
Смещение кривой Гаусса называется эксцессом относительно математического ожидания.

Для избежания эксцесс (Е) и асимметрии (А) используются следующие методы коррекции измерений:

- метод обобщения оценок;

- метод наименьших квадратов (МНК) («Планирование эксперимента при поиске оптимальных условий», Ю.П. Адлер, стр.141);

- устойчивые методы оценивания (УМО).

В зависимости от величины ошибки могут быть приняты различные величины вероятности попадания в ±3δ или достоверности измерения.

P – вероятность попадания измерений в установленные границы измерения (±3δ). Устанавливается заказчиком или нормативными документами.

Типовые значения P:

Р=0,99 - при лабораторных измерениях;

Р=0,95 - при технических измерениях;

Р=0,90 - при технических измерениях новых объектов;

Р=0,82 - критическое значение вероятности, когда устанавливается адекватность математической модели исследуемому объекту или процессу;

Р=0,75 - вероятность для вновь исследуемых объектов или процессов, неизвестных явлений;

Р=0,6; 0,5 - при экспериментальных исследованиях с первичным описанием математической моделью, не определены достаточно точно существенные факторы, влияющие на объект или процесс.

В процессе эксперимента определяется эмпирическая дисперсия S по формуле:

,

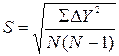где (N-1 ) - потеря статистической степени свободы для расчета Y_i (ν – статистическая степень свободы).

Показатель ассиметрии и эксцесса

Ассиметрия – несоответствие правой и левой ветвей.

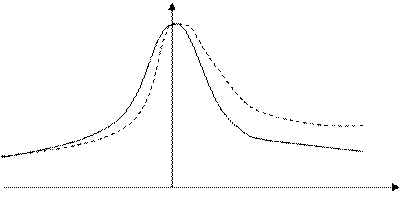
Рис.21. График ассиметрии

Эксцесс – смещение относительно оси.

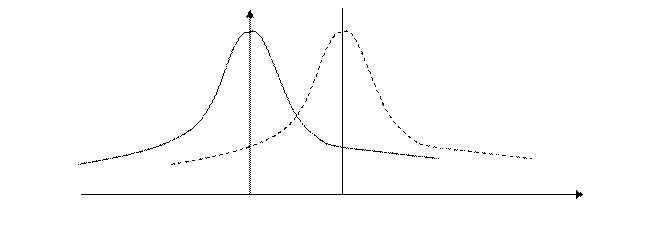
Рис.22. График эксцесс.а

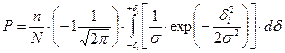
Если кривая Гаусса будет нормальной и соответствовать допустимым значениям вероятности (Р) и эксцесса, то расчет вероятности ведется только с помощью МНК. Этот метод наиболее простой для расчета математической модели и основан на критерии минимальной суммы квадратов отклонений Y (измерений значения выходного параметра) от среднего значения.

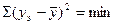
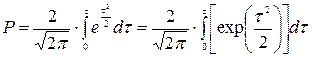
Пример:

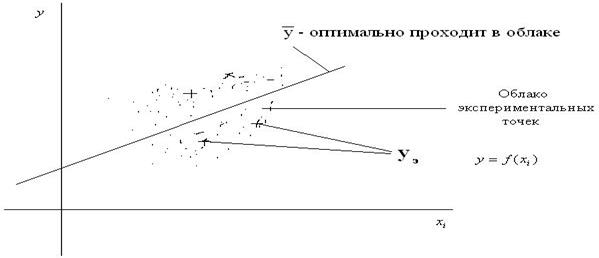
Рис.22. Пример

БЛОК ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ

Рис.23. Блок планирования экспериментальных исследований

Принятие решений перед планированием эксперимента

При выборе области эксперимента, прежде всего надо оценить границы областей определения факторов. При этом должны учитываться ограничения нескольких типов. Первый тип – принципиальные ограничения для значений факторов, которые не могут быть нарушены ни при каких обстоятельствах. Например, если фактор – температура, то нижним пределом будет абсолютный нуль. Второй тип – ограничения, связанные с технико-экономическими соображениями, например, со стоимостью сырья, дефицитностью отдельных компонентов, временем ведения процесса. Третий тип ограничений, с которым чаще всего приходится иметь дело, определяется конкретными условиями проведения процесса, например, существующей аппаратурой, технологией, организацией. В реакторе, изготовленном из некоторого материала, температуру нельзя поднять выше температуры плавления этого материала или выше рабочей температуры данного катализатора.

Оптимизация обычно начинается в условиях, когда объект уже подвергался некоторым исследованиям. Информацию, содержащуюся в результатах предыдущих исследований, будем называть априорной (т.е. полученной до начала эксперимента). Мы можем использовать априорную информацию для получения представления о параметре оптимизации, о факторах, о наилучших условиях ведения процесса и характере поверхности отклика, т.е. о том, как сильно меняется параметр оптимизации при небольших изменениях значений факторов, а также о кривизне поверхности. Для этого можно использовать графики (или таблицы) однофакторных экспериментов, осуществлявшихся в предыдущих исследованиях или описанных в литературе. Если однофакторную зависимость нельзя представить линейным уравнением (в рассматриваемой области), то в многомерном случае, несомненно, будет существенная кривизна. Обратное утверждение, к сожалению, не очевидно.

Итак, выбор экспериментальной области факторного пространства связан с тщательным анализом априорной информации.

После нахождения области факторного пространства надо найти локальную подобласть для планирования эксперимента. Процедура выбора этой подобласти включает два этапа: выбор основного уровня и выбор интервалов варьирования.

Выбор основного уровня. Наилучшим условиям, определенным из анализа априорной информации, соответствует комбинация (или несколько комбинаций) уровней факторов. Каждая комбинация является многомерной точкой в факторном пространстве. Ее можно рассматривать как исходную точку для построения плана эксперимента. Назовем ее основным (нулевым) уровнем. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня.

В разных случаях мы располагаем различными сведениями об области наилучших условий. Если имеются сведения о координатах одной наилучшей точки, и нет информации о границах определения факторов, то остается рассматривать эту точку в качестве основного уровня. Аналогичное решение принимается, если границы известны и наилучшие условия лежат внутри области.

Положение усложняется, если, эта точка лежит на границе (или весьма близко к границе) области. Тогда приходится основной уровень выбирать с некоторым сдвигом от наилучших условий.

Может случиться, что координаты наилучшей точки неизвестны, но есть сведения о некоторой подобласти, в которой процесс идет достаточно хорошо. Тогда основной уровень выбирается либо в центре, либо в случайной точке этой подобласти. Сведения о подобласти можно получить, анализируя изученные ранее подобные процессы, из теоретических соображений или из предыдущего эксперимента.

Наконец, возможен случай с несколькими эквивалентными точками, координаты которых различны. Когда отсутствуют дополнительные данные (технологического, экономического характера и т. д.), выбор произволен. Конечно, если эксперимент недорог и требует немного времени, можно приступить к построению планов экспериментов вокруг нескольких точек.

После того как нулевой уровень выбран, переходим к следующему шагу – выбору интервалов варьирования.