Критерии статистических параметров.
В математической статистике выделяют два фундаментальных понятия: генеральная
совокупность и выборка.
Совокупностью – называется практически счетное множество некоторых объектов или
элементов, интересующих исследователя;
Свойством совокупности называется реальное или воображаемое качество, присущее
некоторым всем ее элементам. Свойство может быть случайным или неслучайным.
Параметром совокупности называется свойство, которое можно квантифицировать в
виде константы или переменной величины.
Простая совокупность характеризуется:
• отдельным свойством (например: все студенты России);
• отдельным параметром в виде константы или переменной (Все студенты женского пола);
• системой непересекающихся (несовместных) свойств, к примеру: Все учителя и ученики школ г. Владивостока.
Сложная совокупность характеризуется:
• системой, хотя бы частично пересекающихся свойств (Студенты психологического и
математических факультетов ДВГУ, окончивших школу с золотой медалью);
• системой параметров независимых и зависимых в совокупности; при комплексном
исследовании личности.
Гомогенной или однородной называется совокупность, все характеристики которой
присущи каждому ее элементу;
Гетерогенной или неоднородной называется совокупность, характеристики которой
сосредоточены в отдельных подмножествах элементов.
Важным параметром является объем совокупности – количество образующих ее
элементов. Величина объема зависит от того, как определена сама совокупность, и какие вопросы нас конкретно интересуют. Допустим нас интересует эмоциональное состояние студента 1-гокурса в период сдачи конкретного экзамена в сессию. Тогда генеральная совокупность исчерпывается в течении получаса. Если нас интересует эмоциональное состояние всех студентов 1-го курса, то совокупность будет гораздо больше, и еще больше, если взять эмоциональное состояние всех студентов 1-го курса данного вуза и т.д. Понятно, что совокупности большого объема можно исследовать только выборочным путем.
Выборкой называется некоторая часть генеральной совокупности, то, что непосредственно изучается. Выборки классифицируются по репрезентативности, объему, способу отбора и схеме испытаний.
Репрезентативная –выборка адекватно отображающая генеральную совокупность в качественном и количественном отношениях. Выборка должна адекватно отображать генеральную совокупность, иначе результаты не совпадут с целями исследования.
Репрезентативность зависит от объема, чем больше объем, тем выборка репрезентативней.
По способу отбора.
Случайная – если элементы отбираются случайным образом. Так как большинство методов математической статистики основывается на понятии случайной выборки, то естественно выборка
должна быть случайной.
Неслучайная выборка:
• механический отбор, когда вся совокупность делится на столько частей, сколько единиц
планируется в выборке и затем из каждой части отбирается один элемент;
• типический отбор – совокупность делится на гомогенные части, и из каждой осуществляется
случайная выборка;
• серийный отбор – совокупность делят на большое число разновеликих серий, затем делают
выборку одной какой-либо серии;
• комбинированный отбор – сочетаются рассматриваемые виды отбора, на разных этапах.
По схеме испытаний – выборки могут быть независимые и зависимые.
По объему выборки делят на малые и большие. К малым относят выборки, в которых
число элементов n ≤ 30. Понятие большой выборки не определено, но большой считается выборка
в которой число элементов > 200 и средняя выборка удовлетворяет условию 30≤ n≤ 200. Это деление условно. Малые выборки используются при статистическом контроле известных свойств уже
изученных совокупностей. Большие выборки используются для установки неизвестных свойств и параметров совокупности.
2. Вероя́тность (вероятностная мера) — численная мера возможности наступления некоторого события.
С практической точки зрения, вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима в случае достаточно большого количества наблюдений или опытов. Например, если среди встреченных на улице людей примерно половина — женщины, то можно говорить, что вероятность того, что встреченный на улице человек окажется женщиной, равна 1/2. Другими словами, оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента.
Согласно определению П. Лапласа, мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель — число всех равновозможных случаев
современном математическом подходе классическая (т. е. не квантовая) вероятность задаётся аксиоматикой Колмогорова. Вероятностью называется мера P, которая задаётся на множестве X, называемом вероятностным пространством. Эта мера должна обладать следующими свойствами.
· 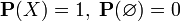 .
.
Вероятностная мера может быть определена не для всех подмножеств множества X. Достаточно определить её на сигма-алгебре Ω, состоящей из некоторых подмножеств множества X. При этом случайные события определяются как измеримые подмножества пространства X, то есть как элементы сигма-алгебры Ω.
Статистический критерий – это решающее правило, обеспечивающее надежное поведение, то есть принятие истинной и отклонение ложной гипотезы с высокой вероятностью″ (Суходольский Г.В.). Статистические критерии обозначают также метод расчета определенного числа и само это число. В большинстве случаев для того, чтобы мы признали различия значимыми, необходимо,
чтобы эмпирическое значение критерия превышало критическое, в некоторых критериях
придерживаются противоположного правила. Эти правила оговариваются в описании каждого
критерия. большинстве случаев, одно и то же эмпирическое значение критерия может оказаться
значимым или незначимым в зависимости от количества наблюдений в выборке (n) или от так
называемого количества степеней свободы, которое обозначается как ν.
Число степеней свободы. Число степеней свободы равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий относятся: объем выборки, средние и дисперсии.
Если мы расклассифицировали наблюдения по классам какой-либо номинативной шкалы и
подсчитали количество наблюдений в каждой ячейке классификации, то мы получаем так называемый частотный вариационный ряд. Единственное условие, которое соблюдается при его
формировании – объем выборки n.
Допустим у нас три класса: ″Умеет работать на ПК – умеет выполнять лишь определенные
операции – не умеет работать″.
Выборка состоит из 50 человек. Если в первом классе – 20 человек, во втором классе – 20
человек, то в третьем должны оказаться 10 человек. Мы ограничены только одним условием –
объемом выборки. Мы не свободны в определении количества испытуемых в третьем классе,
″свобода″ простирается только на первые два класса
ν=с-1=3-1=2
Аналогичным образом, если бы у нас была классификация из 10 разрядов или классов, то мы были бы свободны только в 9 и т.д. Зная n и/или число степеней свободы, по специальным таблицам можно определить критические значения критерия и сопоставить с ними полученное эмпирическое значение.
Среди возможных статистических критериев выделяют: односторонние и двусторонние, параметрические и непараметрические, более и менее мощные.
Односторонние и двусторонние. Понятие одностороннего либо двустороннего критерия связано с формулировкой гипотез. Если ″нулевая″ гипотеза формулируется о равенстве (Х1 = Х2),
то для проверки используется двусторонний критерий. Если же ″нулевая″ гипотеза формулируется
о неравенстве, то возможны три варианта:
1) если Х1≠Х2, то используется двусторонний критерий;
2) если Х1>Х2 или Х1<Х2, то односторонний критерий.
Параметрические критерии – это некоторые функции от параметров совокупности, они
служат для проверки гипотез об этих параметрах или для их оценивания. Параметрические
критерии включают в формулу расчета параметры распределения, т.е. средние и дисперсии.
Непараметрические критерии – это некоторые функции от функций распределения или непосредственно от вариационного ряда наблюдавшихся значений изучаемого случайного
явления. Они служат только для проверки гипотез о функциях распределения или рядах наблюдавшихся значений.
Непараметрические критерии не включают в формулу расчета параметров распределения и основанные на оперировании частотами или рангами. И те, и другие критерии имеют свои преимущества и недостатки.
Параметрические критерии могут оказаться несколько более мощными, чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. Лишь с некоторой натяжкой мы можем считать данные, представленные в стандартизованных оценках, как интервальные. Кроме того, проверка распределения «на нормальность» требует достаточно сложных расчетов, результат которых заранее не известен. Может оказаться, что распределение признака отличается от нормального, и нам так или иначе все равно придется обратиться к непараметрическим критериям. Непараметрические критерии лишены всех этих ограничений и не требуют таких
длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены
лишь в одном – с их помощью невозможно оценить взаимодействие двух или более условий или
факторов, влияющих на изменение признака.
Возможности и ограничения параметрических и непараметрических критериев
| ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ | НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ |
| 1. Позволяют прямо оценить различи* в средних, полученных в двух выборках (t - критерий Стьюдента). | Позволяют оценить лишь средние тенденции, например, ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б - более низкие значения признака (критерии Q, U, φ* и др.). |
| 2. Позволяют прямо оценить различия в дисперсиях (критерий Фишера). | Позволяют оценить лишь различия в диапазонах вариативности признака (критерий φ*). |
| 3. Позволяют выявить тенденции изме-нения признака при переходе от условия к условию (дисперсионный однофакторный анализ), но лишь при условии нормального распределения признака. | Позволяют выявить тенденции изменения признака при переходе от условия к условию при любом распределении признака (критерии тенденций L и S). |
| 4. Позволяют оценить взаимодействие двух и более факторов в их влиянии на изменения признака (двухфакторный дисперсионный анализ). | Эта возможность отсутствует. |
| 5. Экспериментальные данные должны отвечать двум, а иногда трем, условиям: а) значения признака измерены по интервальной шкале; б) распределение признака является нормальным; в) в дисперсионном анализе должно соблюдаться требование равенства дисперсий в ячейках комплекса. | Экспериментальные данные могут не отвечать ни одному из этих условий: а) значения признака могут быть представлены в любой шкале, начиная от шкалы наименований; б) распределение признака может быть любым и совпадение его с каким-либо теоретическим законом распределения необязательно и не нуждается в проверке; в) требование равенства дисперсий отсутствует. |
| 6. Математические расчеты довольно сложны. | Математические расчеты по большей части просты и занимают мало времени (за исключением критериев χ2и λ). |
| 7. Если условия, перечисленные в п.5, выполняются, параметрические критерии оказываются несколько более мощными, чем непараметрические. | Если условия, перечисленные в п.5, не выполняются, непараметрические критерии оказываются более мощными, чем параметрические, так как они менее чувствительны к "засорениям'. |
Уровни статистической значимости.Уровень значимости – это вероятность того, что мы сочли различия существенными, а они на самом деле случайны. Когда мы указываем, что различия достоверны на 5% уровне значимости, или при р≤0,05, то мы имеем ввиду, что вероятность того, что они недостоверны, составляет 0,05. Если же мы указываем, что различия достоверны на 1% уровне значимости, или при р≤0,01, то имеем ввиду, что вероятность того, что они все-таки недостоверны равна 0,01. Иначе, уровень значимости – это вероятность отклонения нулевой гипотезы, в то время
как она верна. Вероятность такой ошибки обычно обозначается как α. Поэтому правильнее указывать
уровень значимости: α≤0,05 или α≤0,01.
Если вероятность ошибки – это α, то вероятность правильного решения равна: 1–α. Чем меньше α, тем больше вероятность правильного решения.
В психологии принять считать низшим уровнем статистической значимости 5%-ный уровень, а достаточным 1%-ный. В таблицах критических значений обычно приводятся значения критериев, соответствующих уровням значимости р≤0,05 и р≤0,01 иногда для р≤0,001. Для некоторых критериев в таблицах указан точный уровень значимости их разных эмпирических значений. Например, для значения критерия Фишера ϕ=1,56 р=0,06.
До тех пор пока уровень значимости не достигнет р=0.05, мы еще не имеем право отклонить нулевую гипотезу. Будем придерживаться следующего правила отклонения гипотезы
об отсутствии различий (Н0) и принятии гипотезы о статистической достоверности различий (Н1).
Исключения: критерий знаков G, критерий Т Вилкоксона и критерий U Манна-Уитни. Для
них устанавливаются обратные соотношения.
Для облегчения принятия решения можно вычерчивать ″ось значимости″. Критические значения критерия обозначены как Q0,05 и Q0,01, эмпирическое значение критерия как Qэмп. Оно заключено в эллипс.
Вправо от критического значения Q0,01 простирается ″зона значимости″ – сюда попадают
эмпирические значения Q, которые ниже Q0.01 и, следовательно, значимые.
Влево от критического значения Q0.05 простирается ″зона незначимости″, – сюда попадают
эмпирические значения Q, которые ниже Q0,05 и, следовательно, незначимы.
В нашем примере, Q0,05 =6; Q0,01=9; Qэмп=8. Эмпирическое значение критерия попадает в область между Q0,05 и Q0,01. Это ″зона неопределенности″: мы уже можем отклонить гипотезу о недостоверности различий (Н0), но еще не можем приять гипотезы об их достоверности (Н1).
Практически, можно считать достоверными уже те различия, которые не попадают в зону
незначимости, сказав, что они достоверны при р≤0,05.

Дата добавления: 2016-11-02; просмотров: 2192;
