Характеристики асимметрии и эксцесса
Мера асимметрии – коэффициент асимметрии (As), рассчитываемый по формуле
Асимметрия характеризует степень асимметричности распределения. Коэффициент
асимметрии изменяется от минус до плюс бесконечности (-∞<As<+∞), для симметричных распределений As=0.
Мера эксцесса (островершинности) – коэффициент эксцесса (Еx), рассчитываемый по
формуле:
Коэффициент эксцесса также изменяется от минус до плюс бесконечности (-∞<Ex<+∞), и
Еx=0 для нормального распределения
Стандартное отклонение это положительное значение квадратного корня из дисперсии:
*
Латинские обозначения:
А - показатель асимметрии распределения
с - количество групп или условий измерения
d - разность между рангами, частотами или частостями
df - число степеней свободы в дисперсионном анализе
Е - показатель эксцесса
F - критерий Фишера для сравнения дисперсий
f - частота
f* - частость, или относительная частота
G - критерий знаков
Н - критерий Крускала-Уоллиса
i - индекс, обозначающий порядковый номер наблюдения
j - индекс, обозначающий порядковый номер разряда, класса, группы
k - количество классов или разрядов признака
L - критерий тенденций Пейджа
М - среднее значение признака или средняя арифметическая; то же, что и х
m - биномиальный критерий
n - количество наблюдений (испытуемых, реакций, выборов и т.п.)
N - общее количество наблюдений в двух или более выборках
Р - вероятность того, что событие произойдет
р - вероятность ошибки 1 рода (то же, что и а), уровень статистической значимости
Q - 1) вероятность того, что событие не произойдет; 2) критерий Розенбаума
rs - коэффициент ранговой корреляции Спирмена
S - критерий Джонкира
S2 - оценка дисперсии
Si - количество значений, которые выше или ниже данного значения
SS - суммы квадратов (в дисперсионном анализе)
Т - критерий Вилкоксона
Тс - суммы рангов по столбцам
Тк - большая сумма рангов в критерии U
U - критерий Манна-Уитни
Wn - размах вариативности, или диапазон значений от наименьшего до
наибольшего
хi - текущее наблюдение; каждое наблюдение по порядку
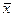- среднее значение признака (то же, что и М)
Греческие обозначения:
α(альфа) - вероятность ошибки I рода (отклонения H0, которая верна)
β (бета) - вероятность ошибки II рода (принятия H0, которая неверна)
λ, (ламбда) - критерий Колмогорова-Смирнова
v (ню) - число степеней свободы в непараметрических критериях
σ (сигма) - стандартное отклонение
φ (фи) - центральный угол, определяемый по процентной доле в критерии φ*
φ* (фи) - критерий Фишера с угловым преобразованием
χ2 (хи-квадрат) - критерий Пирсона
χ2r (хи-ар-квадрат) - критерий Фридмана.
======================================================
| Классификация задач | и методов их решения | |
| Задачи | Условия | Методы |
| 1.Выявление различий в уровне исследуемого признака | а) 2 выборки испытуемых | Q- критерий Розенбаума; U - критерий Манна-Уитни; φ* - критерий (угловое преобразование Фишера) |
| б) 3 и более выборок испытуемых | S - критерий тенденций Джонкира; Н - критерий Крускала-Уоллиса. | |
| 2. Оценка сдвига значений исследуемого признака | а) 2 замера на одной и той же выборке испытуемых | Т - критерий Вилкоксона; G - критерий знаков; φ* - критерий (угловое преобразование Фишера). |
| б) 3 и более замеров на одной и той же выборке испытуемых | χл2 - критерий Фридмана; L - критерий тенденций Пейджа. | |
| 3. Выявление различий в распределении | а) при сопоставлении эмпирического признака распределения с теоретическим | χ2 - критерий Пирсона; λ - критерий Колмогорова-Смирнова; m - биномиальный критерий. |
| б) при сопоставлении двух эмпирических распределений | χ2 - критерий Пирсона; λ - критерий Колмогорова-Смирнова; φ* - критерий (угловое преобразование Фишера). | |
| 4.Выявление степени согласованности изменений | а) двух признаков | rs- коэффициент ранговой корреляции Спирмена. |
| б) двух иерархий или профилей | rs- коэффициент ранговой корреляции Спирмена. | |
| 5. Анализ изменений признака под влиянием контролируемых условий | а) под влиянием одного фактора | S- критерий тенденций Джонкира; L - критерий тенденций Пейджа; однофакторный дисперсионный анализ Фишера. |
| б) под влиянием двух факторов одновременно | Двухфакторный дисперсионный анализ Фишера. |
Дата добавления: 2016-11-02; просмотров: 1049;