Определители и их вычисления
Линейная алгебра
Матрицей размера mxn называется таблица, состоящая из m строк и n столбцов:
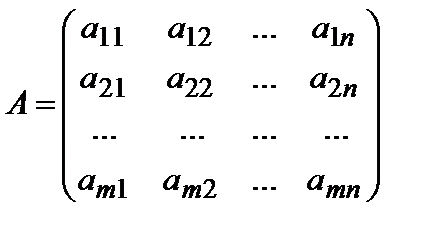 , (6.1.1)
, (6.1.1)
где  - элементы матрицы A, первый индекс i указывает на номер строки, а второй j на номер столбца, на пересечении которых находится элемент
- элементы матрицы A, первый индекс i указывает на номер строки, а второй j на номер столбца, на пересечении которых находится элемент  . В другой записи (1) имеет вид
. В другой записи (1) имеет вид
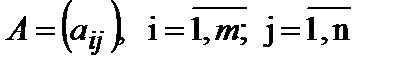 . (6.1.2)
. (6.1.2)
Если m=n, то матрица (1) называется квадратной.
Рассмотрим квадратную матрицу 2-го порядка
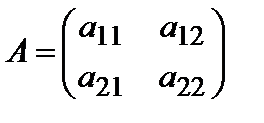 . (6.1.3)
. (6.1.3)
Определителем 2-го порядка, соответствующим квадратной матрице (3), называется число, обозначаемое 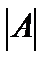 и определяющееся по следующему правилу:
и определяющееся по следующему правилу:
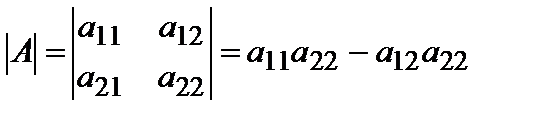 . (6.1.4)
. (6.1.4)
Пример6.1.1. 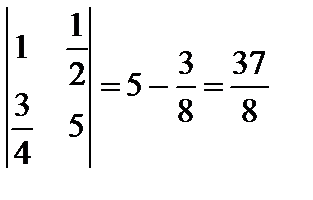 .
.
Определителем 3-го порядка, соответствующим квадратной матрице A третьего порядка 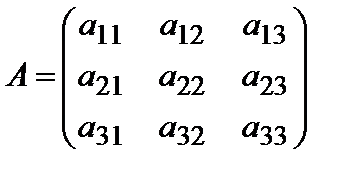 , (6.1.5)
, (6.1.5)
называется число, обозначаемое 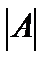 и определяющееся по следующему правилу:
и определяющееся по следующему правилу:
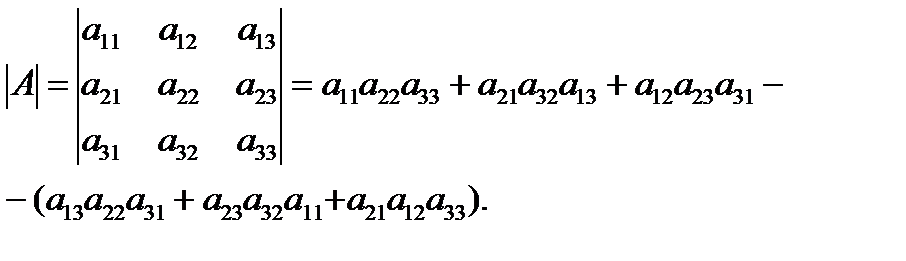 . (6.1.6)
. (6.1.6)
Возьмем определитель 4-го порядка
 (6.1.7)
(6.1.7)
и рассмотрим, например, его элемент  . Мысленно зачеркнем третью строку и первый столбец, на пересечении которых находится этот элемент. Тем самым из оставшихся элементов образуем число
. Мысленно зачеркнем третью строку и первый столбец, на пересечении которых находится этот элемент. Тем самым из оставшихся элементов образуем число
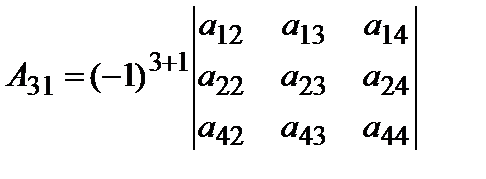 (6.1.8)
(6.1.8)
которое называется алгебраическим дополнением элемента  . Определитель
. Определитель
 , (6.1.9)
, (6.1.9)
называется минором элемента  . Таким образом,
. Таким образом,  .
.
Определитель можно разложить по элементам любой строки или любого столбца.
Например, 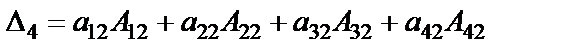 или
или  .
.
Разложение удобно вести по строке (столбцу), где больше нулей.
Квадратная матрица A называется невырожденной (вырожденной), если ее определитель 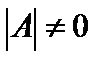 (
( 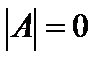 ).
).
Матрица 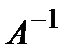 называется обратной к матрице A, если
называется обратной к матрице A, если 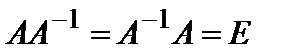 , где E –единичная квадратная матрица.
, где E –единичная квадратная матрица.
 . (6.1.10)
. (6.1.10)
Квадратная матрица A имеет обратную тогда и только тогда, когда она не вырождена.
Дата добавления: 2016-10-17; просмотров: 574;
