Вычисления пределов.
Основные теоремы:
Опр. Предел постоянной величины – есть величина постоянная.
LimС = С
х→а
Если существуют f1(x) и f2(x), то
lim [f1(x) ± f2(x)]= limf1(x) ± limf2(x)
х→а х→а х→а
lim [f1(x)•f2(x)]= lim f1(x) •lim f2(x)
х→а х→а х→а
lim [f1(x) ∕ f2(x)]= lim f1(x) ∕ lim f2(x)] ; lim f2(x)] # 0
х→а х→а х→а х→а
пример.
Найдем придел функции (4х2 -1)/(2х-1)
lim (4х2 -1)/(2х-1) = (2х-1)(2х+1)/(2х-1) =13,
х→6
функция определена в точке х=6
lim (4х2 -1)/(2х-1) = (2х-1)(2х+1)/(2х-1) =2
х→1/2
Функция не определена в (.) х = ½, однако предел функции в этой точке существует и равен 2.
Предполагается, что функция определена во всех точках промежутка, содержащего точку х =а, в самой же точке функция либо определена. Либо не определена.
Бесконечно малые и бесконечно большие функции
Опр.Функция f(x) называется бесконечно малой (Б.М.)при х→а, если
lim f(x)= 0
х→а
пр. lim х2 -4 =0 - Б.М.
х→2
lim х2 -4 =-3 не является - Б.М.
х→1
Опр. Функция f(x) называется бесконечно большой , если
lim f(x)= ∞ Б.Б.
х→а
Аналогично определяются Б.М. и Б.Б. функции при х→∞.
Между Б.М. и Б.Б. функциями существует тесная связь, которая выражается следующими теоремами.
1. Функция обратная по величине бесконечно большой, является бесконечно малой величиной.
2. Функция обратная по величине бесконечно малой. Называется бесконечно большой величиной.
3. Бесконечно малые величины обладают следующими свойствами:
1) Сумма или разность двух бесконечно малых функций есть величина бесконечно малая.
2) Произведение Б.М. функции на функцию ограниченную Х на постоянную или Б.М. функцию есть функция бесконечно малая.
Бесконечно большие функции обладают следующими свойствами:
1). Сумма Б.Б. функции и функции ограниченной есть функция Б.Б. того же знака.
2). Сумма двух бесконечно больших функций одинакового знака есть функция бесконечно большая.
3). Произведение Б.Б. функции на Б.Б. функцию есть функция Б.Б.
Техника вычисления пределов
Подставить значение, к которому стремиться х в функцию. Если предел вычисляется, то полученное значение и будет пределом данной функции.
Чему равен предел: Lim 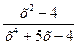
х→1
Если предел не вычисляется, то надо применить определенную технику
Могут возникнуть неопределенности: ∞/∞; 0/∞; 0/0 и т.д.
1. Деления на максимальную степень.
Чему равен предел: Lim 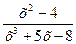
х→ ∞
2. Разложение квадратного трехчлена на множители
Чему равен предел: Lim 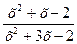
х→ -2
Левый и правый предел функции
Опр. Если число А1 есть предел функции при х→а, так, что х принимает только значения > a, то число А1 называется правым пределом функции.
lim f(x)= А1
х→а+0
аналогично:
Опр. Если число А2 есть предел функции при х→а, так, что х принимает только значения < a, то число А2 называется левым пределом функции.
lim f(x)= А2 Если А1 = А2= А, то это предел функции
х→а-0
Примеры :В. А. Подольский № 7.46,7.47;7.48;7.51
Пр. Найти придел функции у = 1/(х+2)
lim 1/(х+2) = - ∞
х→-2-0
lim 1/(х+2) = + ∞
х→-2+0
Найти придел функции у = х/(х-3)
lim х/(х-3) = + ∞ lim х/(х-3) = - ∞
х→-3-0 х→-3+0
Непрерывность и точки разрыва
1. Приращение аргумента и приращение функции
Если х1 и х2 –значения аргумента х, а f(x1) и f(x2) значения функции y=f(x), то ∆х= x2 – x1, называется приращением аргумента на отрезке [x2 , x1], а величина ∆у= f(x2) - f(x1)=f(x+∆х) –f(x) , ∆у – приращение функции на этом отрезке.
Пример:
Вычислить приращение аргумента и приращение функции у=х2-2х+3
а) от х1=0 до х2=1;
б) от х1=-1 до х2=3;
а) ∆х= x2 – x1 =1- 0 = 1; ∆у = 1-2+3-3= -1
б) ∆х= x2 – x1 = 3-(-1) = 4; ∆у = 9-6+3-(1+2+3) = 0
пр. 7.175; 7.178-7.180
Первое определение непрерывности
Функция y=f(x) называется непрерывной в (.) х= а, если бесконечно малому приращению аргумента в этой точке, соответствует бесконечно малое приращение функции.
lim ∆у = 0
∆х→а
Второе определение непрерывности
Функция y=f(x) называется непрерывной в (.) х= а, если:
- она определена в (.) х= а, т.е существует ее значение в (.) х= а, равное f(а);
- существует конечный предел функции в этой точке, т.е. lim f(x)= А;
х→а
- этот предел равен значению функции в (.) х= а, т.е. . lim f(x)= А= f(а).
х→а
Примером непрерывности функции может служить любая элементарная функция. Которая непрерывна в каждой точке своей области определения.
Точка х=а называется точкой разрыва функции y=f(x), если эта функция определена в некоторой окрестности точки х= а, но в самой точке х= а не удовлетворяет условию непрерывности.
Точки разрыва функции делятся на два типа. К точкам разрыва первого рода относятся такие точки, в которых существуют конечные односторонние пределы (левый и правый предел).
К точкам разрыва второго рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.
Точки разрыва первого рода делятся в свою очередь на точки. В которых разрыв устраним, когда lim f(x)= lim f(x) ≠ f(а) х→а-0 х→а+0
И на точки скачка функции, когда lim f(x)= lim f(x) ≠ f(а)
х→а-0 х→а+0
а разность f(а+0) - f(а+0) называется скачком функции в точке х= а.
Пр.Исследовать функцию на разрыв у = 1/(х+3)
ООФ функция определена при х€ ( -∞;-3 ) (-3; +∞)
Найдем левый и правый пределы
lim 1/(х+3) = - ∞
х→-3-0
lim 1/(х+3) = + ∞
х→-3+0
Данная функция имеет разрыв второго рода в точке х=-3, т.к. левый и правый пределы бесконечны.
Рис.
Пр. Исследовать функцию на разрыв у =1/(1+21/х)
ООФ х ≠ 0
lim 1/(1+21/х) = 1
х→-- 0
lim 1/(1+21/х) = 0
х→-+ 0
Данная функция имеет разрыв первого рода в точке х=0, так-так левый и правый придел имеют конечные значения. Имеется скачек функции.
Рис.
Пр.Исследовать функцию на разрыв у = 1/(х+5)2
ООФ функция определена при х€ ( -∞;-5 ) (-5; +∞)
Найдем левый и правый пределы
lim 1/(х+5)2 = + ∞
х→-5-0
lim 1/(х+5)2 = + ∞
х→-5+0
Данная функция имеет разрыв второго рода в точке х = -5, т.к. левый и правый пределы бесконечны.
Рис.
 Пр. Исследовать функцию на разрыв
Пр. Исследовать функцию на разрыв
х при х ≤ 0
х2 при 0 < х ≤ 1
x +1 при х >1
Найдем левые и правые приделы в точках изменения функции:
lim х2= 1 lim х+1= 2 lim х2= 0 lim х = 0
х→1—0 х→1+ 0 х→+ 0 х→- 0
Функция имеет разрыв 1-го рода со скачком функции в точке х =1
Рис.
Пр . Исследовать функцию на разрыв у =31/х
ООФ х ≠ 1
Найдем левые и правые приделы
lim 31/х = 0
х→- 0
lim 31/х = +∞
х→+0
Данная функция имеет разрыв второго рода в точке х = 0, т.к. правый предел бесконечен.
Дата добавления: 2016-09-20; просмотров: 924;
