Вычисление пределов.

Одной из важных задач математического анализа является вычисление пределов последовательностей и функций [99,103,113,187,190,221]. Для решения этой задачи в системе MATLAB предусмотрена функция:

limit(func [, x, b, options])

где func – символьная запись функции или ее имя; x – имя переменной относительно которой вычисляется предел; b – точка в которой вычисляется предел (возможно вычисление справа и слева от заданной точки).

Рассмотрим использование функции limit на нескольких примерах.

Пусть требуется вычислить предел

.

Имеем:

>> syms x h

>> limit((cos(x+h)-cos(x))/h,h,0)

ans =

-sin(x)

Функция limit(func,x,a) возвращает предел символьного выражения func в точке x, стремящейся к значению a.

Пусть требуется вычислить предел

.

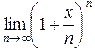Имеем:

>> syms x n

>> limit((1+x/n)^n,n,inf)

ans =

exp(x)

Функция limit(func,x,inf) возвращает предел символьного выражения func в точке x, стремящейся к бесконечности.

Пусть требуется вычислить предел

.

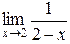Имеем:

>> syms x

>> limit(1/(2-x),x,2)

ans =

NaN

Поясним, что значение NaN переменной ans в данном случае означает, что значение рассматриваемого предела не определено.

Пусть требуется вычислить пределы

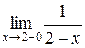и .

И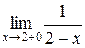меем:

>> syms x

>> limit(1/(2-x),x,2,'left')

ans =

Inf

>> limit(1/(2-x),x,2,'right')

ans =

-Inf

Функция limit(func,x,a,’right’) возвращает предел символьного выражения func в точке x, стремящейся к значению a справа (т.е. x принимает значения большие, чем a). Функция limit(func,x,a,’left’) возвращает предел символьного выражения func в точке x, стремящейся к значению a слева (т.е. x принимает значения меньшие, чем a).

Пусть требуется вычислить пределы слева и справа:

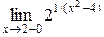и .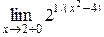

Имеем:

>> syms x

>> f=2^(1/(x^2-4))

f =

2^(1/(x^2 - 4))

>> limit(f,x,2,'left')

ans =

>> limit(f,x,2,'right')

ans =

Inf