Виды средних и способы их вычисления
Правильное применение средних возможно лишь на основе предварительной группировки: выделения качественно однородных совокупностей и расчленения явления на части в зависимости от различия условий, под влиянием которых явление складывается.
Под средней величиной в статистике понимают показатель, который характеризует типичный уровень изменяющегося признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
При изучении отдельных видов средних величин рекомендуется четко представлять методику их расчета и область применения. Наиболее распространенной формой средних величин является средняя арифметическая, расчет которой производится путем деления суммы всех значений изучаемого признака на их количество.
Формула расчета:

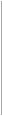
| å xi | |||||
| x = | , | (5.1) | |||
| n | |||||

где х – среднее значение изучаемого признака; xi –конкретное значение этого признака;
n –число единиц,значение признака которых изучается.

Расчет средней по данной формуле называется способом простой средней арифметической.
Если какое-то значение признака повторяется у нескольких единиц, то в этом случае формула расчета средней арифметической имеет такой вид:
| åxi fi | ||||||
| x = | , | (5.2) | ||||
| å fi | ||||||
 где fi – частота повторения отдельных вариантов признака.
где fi – частота повторения отдельных вариантов признака.

Данная формула носит название средней арифметической взвешенной.
Средняя хронологическая используется в тех случаях, когда имеются данные наблюдения на определенные моменты времени; ее расчетная формула имеет вид:
| = 0.5x1 + x2 + x3 ++ xn -1 + 0.5xn, | ||||
| x | (5.3) | |||
| n -1 | ||||

Средняя геометрическая используется для анализа темпов роста явлений и вычисляется по следующим формулам:
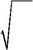






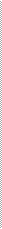
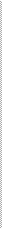
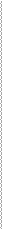
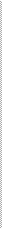
| xn | |||||||||
| x = n-1 | , | ||||||||
| x | |||||||||
| x = n-1 k ×k ×k × | ×k | , | |||||||
| n-1 |

где x1 – первый (базисный) уровень ряда динамики; xn –последний уровень ряда динамики;
n –число уровней(или периодов);
k1, k2,…, kn-1–цепные коэффициенты роста данного ряда динамики.
(5.4)
(5.5)
Взвешенные средние широко применяются при обработке данных текущего наблюдения по производственным участкам и цехам предприятия, обобщении материалов отчетности предприятий и организаций.
Средняя гармоническая взвешенная определяется по формуле:
| Х=М / (М / х), | (5.6) |
где М=х∙f

Пример.
| Партия | Себестоимость одной детали, | Затраты на всю партию деталей, |
| деталей | руб. (х) | руб. (М) |
| 1,8 | ||
| 2,0 | ||
| 2,3 | ||
Х=М / (М / Х) = (180+400+165) / (180/1,8+400/2+165/2,3) =1,98 (руб.).
Средняя себестоимость единицы продукции исчислена по формуле средней гармонической, так как исходной базой исчисления средней себестоимости является отношение затрат на производство всей продукции к количеству единиц продукции.
Выбор вида средней зависит от задачи, стоящей перед исследователем, и характера исходных данных. Если имеются варианты и частота, то для расчета средней величины применяется средняя арифметическая. В тех случаях, когда имеются варианты и произведения вариант на частоты (х∙f), а частоты неизвестны, для расчета средней величины используется средняя гармоническая.
Средняя гармоническая используется в тех случаях, когда следует исчислить среднюю из величин, обратно пропорциональных изучаемому явлению.
Дата добавления: 2016-10-17; просмотров: 833;
