Структурные средние
Особого рода средними, используемыми в экономическом анализе для изучения структуры вариационного ряда, являются мода и медиана.
Медиана –это значение признака у той единицы совокупности,которая расположена всередине упорядоченного ряда. По данным интервального вариационного ряда, который предварительно ранжирован, медиану определяют по формуле:
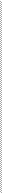


| Me = x + d | (0.5å f i )- Sm-1 | , | (5.7) | |
| fm | ||||
где x0 – нижняя граница медианного интервала; d –величина медианного интервала;
0.5å fi – полусумма частот всех интервалов;
Sm-1–сумма частот до медианного интервала; fm –частота медианного интервала.


Если ряд дискретный, то медианой является срединное значение признака, и применение формулы не требуется.
Мода –это наиболее часто встречающееся значение признака.В интервальномвариационном ряду ее определяют по формуле:
| Mo = x0 | + d | f 2 | - f1 | , | (5.8) | |||
| ( f 2 | - f1) | +( f | 2- f3) | |||||

где x0 – нижняя граница модального интервала; d –величина модального интервала;
f2–частота модального интервала;
f1–частота интервала,предшествующего модальному; f3–частота интервала,следующего за модальным.

В дискретном ряду мода – это вариант признака, имеющий наибольшую частоту.
Дата добавления: 2016-10-17; просмотров: 491;
