Понятие о сдвиге. Расчет заклепок на перерезывание.

Мы изучали, что при простом растяжении или простом сжатии две части стержня, разделенные наклонным сечением, стремятся не только оторваться друг от друга, но и сдвинуться одна относительно другой. Растяжению сопротивляются нормальные, а сдвигу — касательные напряжения.

На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига.

В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень' заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).

Для изучения работы заклепок рассмотрим простейший пример заклепочного соединения (Рис.1). Шесть заклепок, расположенных в два ряда, соединяют два листа внахлестку. Под действием сил Р эти листы стремятся сдвинуться один по другому, чему препятствуют заклепки, на которые и будет передаваться действие сил ).

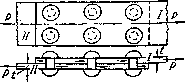
Рис.1. Расчетная схема заклепочного соединения

Для проверки прочности заклепок применим общий порядок решения задач сопротивления материалов.

На каждую заклепку передаются по две равные и прямо противоположные силы: одна—от первого листа, другая — от второго. Опытные исследования показывают, что одни из заклепок ряда нагружаются больше, другие — меньше. Однако к моменту разрушения усилия, передающиеся на различные заклепки, более или менее выравниваются за счет пластических деформаций. Поэтому принято считать, что все заклепки работают одинаково. Таким образом, при 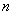заклепках в соединении, изображенном на фиг. 1, на каждую из них действуют по две равные и противоположные силы 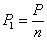(Рис.2); эти силы передаются на заклепку путем нажима соответствующего листа на боковую полуцилиндрическую поверхность стержня. Силы 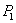стремятся перерезать заклепку по плоскости mk раздела обоих листов.

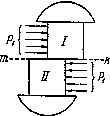
Рис.2. Силы, действующие на заклепочное соединение.

Для вычисления напряжений, действующих по этой плоскости, разделим мысленно заклепочный стержень сечением mk и отбросим нижнюю часть (Рис.2). Внутренние усилия, передающиеся по этому сечению от нижней части на верхнюю, будут уравновешивать силу 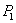т. е. будут действовать параллельно ей в плоскости сечения, и в сумме дадут равнодействующую, равную 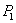. Следовательно, напряжения, возникающие в этом сечении и действующие касательно к плоскости сечения, это — касательные напряжения 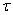. Обычно принимают равномерное распределение этих напряжений по сечению. Тогда при диаметре заклепки d на единицу площади сечения будет приходиться напряжение:

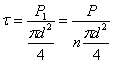
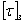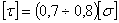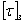Величина допускаемого касательного напряжения , или, как говорят, допускаемого напряжения на срез, принято определять в виде: Зная , мы напишем условие прочности заклепки на перерезывание в таком виде:

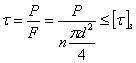
т. е. действительное касательное напряжение 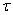в материале заклепки должно быть равно допускаемому 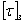или меньше его.

Из этого условия можно определить необходимый диаметр заклепок, если задаться их числом, и наоборот. Обычно задаются диаметром заклепочных стержней d в соответствии с толщиной t склепываемых частей (обычно 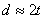) и определяют необходимое число заклепок :

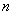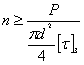
Знаменатель этой формулы представляет собой ту силу, которую безопасно может взять на себя каждая заклепка.

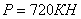
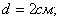
Пусть 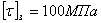; тогда

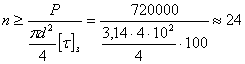
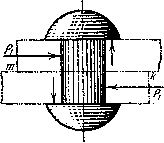
Рис.3. Расчетная модель действия нормальных напряжений

При выводе формулы расчета заклепки на перерезывание, помимо оговоренных, допущена еще одна неточность. Дело в том, что силы 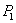действующие на заклепку, не направлены по одной прямой, а образуют пару. Эта пара уравновешивается другой парой, образующейся из реакций соединенных листов на головку заклепки (Рис.3) и ведет к появлению нормальных напряжений, действующих по сечению mk.

Кроме этих нормальных напряжений, по сечению mk действуют еще нормальные напряжения, вызванные тем, что при охлаждении заклепочный стержень стремится сократить свою длину, чему мешает упор головок заклепки в листы. Это обстоятельство, с одной стороны, обеспечивает стягивание заклепками листов и возникновение между ними сил трения, с другой — вызывает значительные нормальные напряжения по сечениям стержня заклепки. Особых неприятностей эти напряжения принести не могут. На заклепки идет сталь, обладающая значительной пластичностью; поэтому даже если бы нормальные напряжения достигли предела текучести, можно ожидать некоторого пластического удлинения стержня заклепки, что вызовет лишь уменьшение сил трения между листами и осуществление в действительности той схемы работы заклепки на перерезывание, на которую она и рассчитывается. Поэтому эти нормальные напряжения расчетом не учитываются.

Лекция № 24. Расчет заклепок на смятие и листов на разрыв.

Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.

Так как передача сил на заклепочный стержень происходит путем нажатия стенок заклепочного отверстия на заклепку, то необходимо установить, не произойдет ли наружное обмятие этого стержня или стенок отверстия, — произвести проверку на смятие.

На рис.1 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению 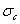в точке А поверхности заклепки.

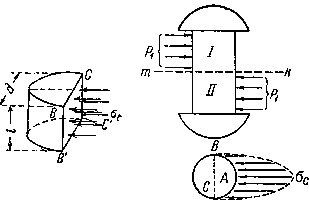
Рис.1. Передача давлений на стержень заклепки.

Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки.

Так как давление на одну заклепку равн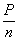о , то

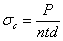
условие прочности на смятие будет иметь вид:

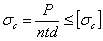
где 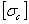— допускаемое напряжение на смятие. Отсюда необходимое число заклепок

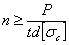
Допускаемое напряжение на смятие принимают обычно в 2 — 2,5 раза больше основного допускаемого напряжения на растяжение и сжатие 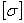, так как расчет на смятие по существу является упрощенной проверкой прочности по контактным напряжениям.

Таким образом определяется число заклепок, необходимое для прочного соединения листов. Из двух полученных значений 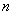, конечно, надо взять большее.

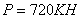
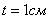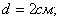
Если мы вернемся к рассмотренному ранее примеру и примем , ,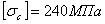то получим:

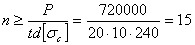
Таким образом, условие прочности заклепок на перерезывание требует постановки двадцати четырех заклепок; условие же прочности на смятие — пятнадцати заклепок. Очевидно, необходимо поставить двадцать четыре заклепки. В этом примере работа заклепок на срез оказывается опаснее работы их на смятие. Это обычно бывает в соединениях с так называемыми односрезными заклепками, в которых каждая заклепка перерезывается в одной плоскости.

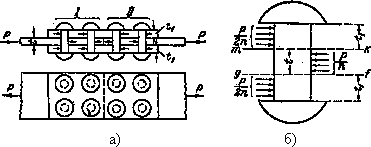
а) расчетная схема, б) действующие усилия
Рис.2. Соединение с накладками:

В несколько других условиях будут работать заклепки соединения, показанного на Рис.2а. Здесь стык двух листов осуществлен при помощи двух накладок. Сила Р при помощи первой группы заклепок передается от левого листа обеим накладкам, а от последних при помощи второй группы заклепок передается правому листу.

Называя через 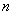число заклепок, необходимое для передачи усилия Р от листа на накладки и от накладок на другой лист, получаем, что на каждую заклепку передается усилие от основного листа 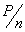. Оно уравновешивается усилиями 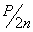, передающимися на заклепку от накладок (Рис.2б).

Стержень заклепки теперь подвергается перерезыванию уже в двух плоскостях; средняя часть заклепки сдвигается влево. Допускают, что срезывающая сила 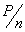равномерно распределяется по двум сечениям, 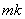и gf. Напряжение 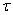и условие прочности для двухсрезной заклепки принимает вид:

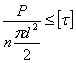и

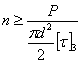
Таким образом, при двойном перерезывании число заклепок по срезыванию оказывается в два раза меньше, чем при одиночном перерезывании.

Переходим к проверке на смятие. Толщина склепываемых листов 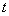; толщина накладок 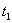не должна быть меньше 0,5t, так как две накладки должны взять от основного листа всю силу Р. Поэтому:

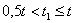
Сила 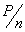сминает и среднюю часть заклепки и верхнюю с нижней. Опаснее будет смятие той части, где площадь смятия меньше.

Так как толщина среднего листа не больше суммы толщин обеих накладок, то в худших условиях по смятию будет средняя часть заклепки. Условие прочности на смятие останется таким же, как и при односрезных заклепках:

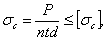
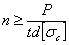
Таким образом, для рассматриваемой конструкции число заклепок в первой и во второй группах определится из полученных условий.

Пусть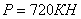

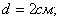
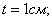
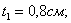
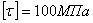
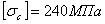
Тогда:

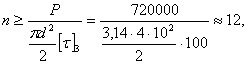
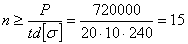
В этом случае при двухсрезных заклепках условия их работы на смятие тяжелее, чем на срезывание; следует принять .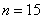

На двух рассмотренных примерах мы установили общие методы проверки прочности заклепочных соединений. В металлических конструкциях иногда приходится склепывать целые пакеты соединяемых элементов. В таких пакетах заклепки могут работать и на большее число срезов. Однако методы расчета многосрезных заклепок не отличаются от изложенных. Для вычисления касательных напряжений следует разделить силу, относящуюся к одной заклепке, на суммарную площадь среза, воспринимающую эту силу. Для вычисления же напряжений смятия следует найти ту часть заклепки, которая находится в наиболее опасных условиях, т. е. воспринимает наибольшую силу на наименьшем протяжении. Напряжения смятия получаются делением этой силы на площадь диаметрального сечения наиболее напряженной части заклепки. Затем останется написать два условия прочности и получить .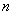

Наличие заклепок вносит некоторые изменения и в проверку прочности на растяжение или сжатие самих склепанных листов. Опасным сечением каждого листа (Рис.3) будет теперь сечение, проходящее через заклепочные отверстия; здесь рабочая ширина листа будет наименьшей; принято говорить, что это сечение ослаблено заклепочным отверстием. Называя полную ширину листа b, получаем для него такое условие прочности:

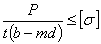
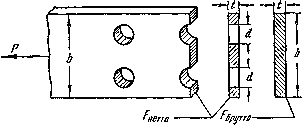
Рис.3. Расчетная модель листа на разрыв.

где 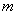— число отверстий, попадающих в сечение (в нашем случае — два).

Отсюда можно найти величину 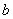, задавшись толщиной листа t. Площадь 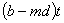ослабленного сечения называется площадью нетто, площадь же полного сечения листа 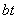называется площадью брутто.

Этот учет влияния заклепочных отверстий на прочность склепываемых листов общепринят, но является весьма условным. На самом деле, влияние отверстия в листе вызывает у его краев, на концах диаметра, перпендикулярного к направлению растяжения, значительные местные напряжения, которые могут достичь предела текучести материала и вызвать остаточные деформации, захватывающие, однако, весьма небольшой объем материала листа.

Некоторую опасность в отношении образования трещин эти местные напряжения могут представить лишь при действии переменных нагрузок в материале, имеющем низкий предел усталости. Однако в обычных условиях работы заклепочных соединений эта опасность может считаться исключенной. Во избежание возможности разрушения листов заклепками заклепки размещаются на определенных расстояниях друг от друга и от края листа.

Расположение заклепок в плане производится как по условиям обеспечения прочности и плотности соединения, так и по чисто производственным соображениям. Расстояния между центрами заклепок принимаются не менее 3d и не более 7d. Расстояния до края листов должны быть не менее 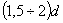(Рис.4). Чтобы длина стыка была возможно меньше, берут 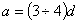, а в целях меньшего ослабления сечения расстояние е берут возможно большим (до 7d), что позволяет уменьшить число рядов, а следовательно, и ослабление.

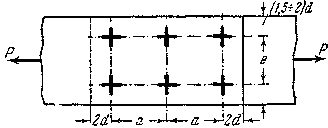
Рис.4. Практические рекомендации по расположению заклепок в соединении.

При проектировании заклепочных соединений для котлов и резервуаров, где добиваются плотных швов, помимо расчета на срез производят проверку сопротивления скольжению за счет трения. Однако допускаемое напряжение по скольжению дается в МПа поперечного сечения заклепки; таким образом, проверка на трение при односрезных заклепках сводится к проверке на срез лишь с другим допускаемым напряжением. При двухсрезных заклепках в расчет на трение вводится, конечно, одна площадь сечения заклепки, но зато повышается почти вдвое допускаемое напряжение на трение за счет двух накладок.

Поэтому так называемый расчет заклепок на трение является, по существу, проверкой прочности на срез с другими лишь допускаемыми напряжениями на квадратный сантиметр площади поперечного сечения заклепки.

Правильнее было бы сохранить лишь один метод проверки заклепочных соединений на смятие и срез, учитывая влияние сил трения при назначении допускаемых напряжений в зависимости от способа клепки, качества отверстий и требований, предъявляемых ко шву в отношении плотности.

В заклепочных соединениях для котлов принимают обычно допускаемое напряжение на скольжение (на 1 см² площади заклепки):

• от 50 до 70 МПа при швах внахлестку,
• 90 120 с двумя накладками.

При проверке по этим данным, очевидно, надо вести расчет, как при заклепках одиночного перерезывания, с допускаемым напряжением от 50 до 70 или от 90 до 120МПа.

Лекция № 25. Расчет сварных соединений.

При изготовлении металлических конструкций часто применяется сварка с помощью электрической дуги.

Впервые электрическая дуга была открыта русским ученым проф. В. В. Петровым в 1802 г. Обнаружив плавление металла в пламени полученной им электрической дуги, проф. Петров указал на возможность использования этого явления в технике. Однако электрическая дуговая сварка была изобретена лишь в конце XIX века русскими инженерами Н. Н. Бенардосом (1882 г.) нашим земляком и Н. Г. Славяновым (1888 г.) и получила впоследствии широкое распространение во всем мире.

Сущность электросварки по методу Славянова заключается в том, что, расплавляя электрической дугой материал электрода (сталь), заполняют им стык соединяемых элементов, также прогреваемых дугой до температуры плавления. В результате, после остывания расплавленного металла, образуется шов, прочно соединяющий стыкуемые элементы. Схема сварки показана на Рис.1. Электрическая дуга горит между металлическим электродом и свариваемым металлом, расплавляя электрод и кромки соединяемых элементов металла, между которыми образуется так называемая сварочная ванна.

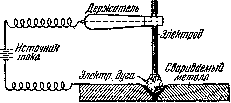
Рис.1. Технологическая схема сварки.

Для защиты плавящегося металла от попадания вредных включений из окружающего воздуха на поверхность электрода наносится толстая защитная обмазка, выделяющая при плавлении электрода большое количество шлака и газов, благодаря чему плавящийся металл изолируется от окружающего воздуха.

Этим обеспечивается высокое качество металла сварного шва, механические свойства которого могут резко ухудшиться под влиянием кислорода и азота воздуха (при отсутствии обмазки или при тонкой обмазке). С той же целью автоматическая сварка производится под слоем флюса, защищающим плавящийся металл от попадания кислорода и азота воздуха.

При правильном выборе конструкции соединений, материалов и технологии сварки сварные соединения по надежности не уступают заклепочным при действии как статических, так и динамических нагрузок (в том числе ударных и знакопеременных). В то же время электросварка имеет ряд преимуществ перед клепкой, из которых важнейшими являются меньшая трудоемкость сварочных работ и отсутствие ослабления сечений соединяемых элементов отверстиями. Это дает значительную экономию средств и металла, помимо экономии, получаемой за счет большей компактности соединений. Большие экономические выгоды, приносимые электросваркой, и даваемое ею упрощение конструкций привели в последнее время к постепенному вытеснению заклепочных соединений сварными.

Значительное развитие электросварка получила в СССР благодаря трудам советских ученых Патона, Вологдина, Никитина, Хренова и др., разработавших новые методы сварки, обеспечивающие высокую прочность соединений.

Методы расчета сварных соединений тесно связаны с технологией сварки, причем для многих видов соединений расчет носит весьма условный характер. Вообще методику расчета сварных соединений нельзя еще считать установившейся.

Что касается норм допускаемых напряжений для материала швов, то они принимаются различными в зависимости от способа сварки (ручная и автоматическая), а также от состава и толщины защитной обмазки электродов.

В таблице приведены допускаемые напряжения для сварных швов в конструкциях из стали марки ст. 3 по существующим нормам.

Таблица. Допускаемые напряжения при сварке.

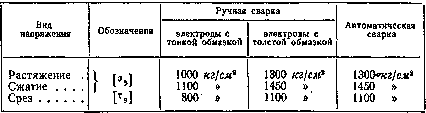
При проверке прочности сварных швов учитывается возможный непровар в начале шва и образование кратера в конце. Поэтому расчетная длина шва принимается меньшей, чем действительная или проектная на 10 мм.

Необходимо отметить, что наиболее простым и надежным видом соединения является соединение встык, образуемое путем заполнения зазора между торцами соединяемых элементов наплавленным металлом. Соединение встык осуществляется, в зависимости от толщины соединяемых элементов, по одному из типов, показанных на Рис.2. Проверка прочности производится на растяжение или сжатие по формуле:

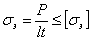
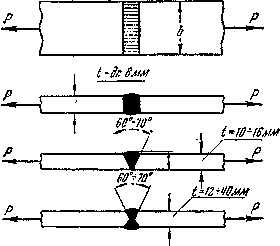
Рис.2. Расчетная схема сварного соединения.

Здесь 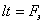—условная рабочая площадь сечения шва, где расчетная длина шва 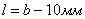, а высота шва h принимается равной толщине свариваемых элементов t.

Поскольку допускаемое напряжение для сварного шва ниже, чем для основного металла, стремятся к увеличению длины стыкового шва. С этой целью применяют соединение встык с косым швом (Рис.3). Исследования таких соединений, произведенные Институтом электросварки Академии наук УССР, показали, что равнопрочность их с основным металлом всегда обеспечивается.

Проверка прочности косых швов производится и по нормальным и по касательным напряжениям, возникающим по сечению шва mn:

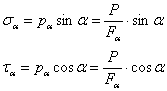
Рис.3. Расчетная схема косого сварного соединения.

Имея в виду, что 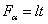получим:

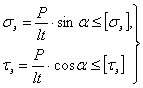
(10.10)

Здесь расчетная длина шва по техническим условиям принимается равной .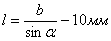

Как установлено опытом, наиболее рациональным углом наклона шва к линии действия сил является 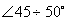. Недостатком соединения косым швом является неудобство центрировки стыкуемых элементов при сварке, поэтому его применяют редко.

Иногда соединение листов производится внахлестку или встык с перекрытием накладками. Это вызывает необходимость сваривать листы, не лежащие в одной плоскости, что осуществляется при помощи так называемых валиковых (или угловых) швов — лобовых или торцевых (перпендикулярных к направлению действующей силы) и боковых или фланговых (параллельных ей).

Валиковый шов в сечении имеет довольно неопределенную форму (Рис.104). В теоретических расчетах на прочность сечение шва принимается в виде равнобедренного треугольника (очерченного пунктиром) с расчетной высотой ).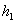

а) технология. б) расчетная схема
Рис.4. Сварное соединение внахлестку:

Соединения торцевыми(лобовыми) швами показаны на рис.5. Разрушение таких швов происходит по наиболее слабому сечению AB, как это установлено опытами.

Рис.5. Сварное соединение торцевыми швами.

Как это видно из рис. 4 б, полное напряжение, возникающее в сечении АВ, может быть разложено на нормальную и касательную составляющие. Поскольку сопротивление стали сдвигу ниже, чем при растяжении, расчет лобовых швов производится условно на срез в предположении равномерного распределения касательных напряжений по площади сечения АВ. Имея в виду, что на восприятие силы Р в этих соединениях (Рис.5) работают два лобовых шва, верхний и нижний, получим:

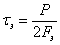
Так как площадь сечения шва 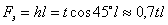, а расчетная длина 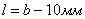, то условие прочности примет вид:

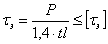
В действительности, материал шва испытывает сложное напряженное состояние, причем напряжения по сечению АВ распределяются неравномерно. Исследования, произведенные методами теории упругости и подтвержденные экспериментально, показали, что в углах шва имеет место высокая концентрация напряжений.

Если учесть, что, вследствие укорочения швов при остывании, в зоне сварки возникают дополнительные напряжения и в основном металле, ведущие к переходу его в хрупкое состояние, то следует иметь в виду, что концентрация напряжений может явиться причиной появления трещин в основном металле соединения.

Поэтому такое соединение не может быть рекомендовано, особенно при переменной или ударной нагрузке. Значительно надежнее работа соединения встык без накладок.

Соединение фланговыми (или боковыми) швами показано на Рис.6 а. Разрушение шва, показанное на Рис.6 б, происходит на значительном его протяжении путем срезывания наплавленного металла в направлении, параллельном шву по наиболее слабой плоскости АВ.

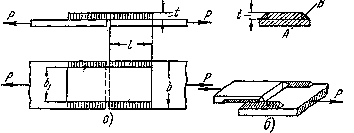
Рис.6. Соединение фланговыми швами- а) и его разрушение б)

Условие прочности для двух симметрично расположенных швов имеет вид:

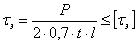
Если стык перекрыт двухсторонними накладками, число швов удвоится и условие прочности примет вид:

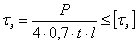
Отсюда обычно определяют необходимую расчетную длину 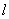фланговых швов. Проектная же длина каждого шва принимается равной .

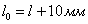Как показали опыты, разрушение фланговых швов происходит по типу разрушений пластичных материалов со значительными остаточными деформациями. Это делает работу фланговых швов более благоприятной, чем работу лобовых швов. Однако следует иметь в виду, что у концов фланговых швов также имеет место высокая концентрация напряжений.

При проектировании часто стремятся обеспечить большую надежность соединения, применяя вместо сварки встык, или в дополнение к ней, перекрытие стыка накладками, которые привариваются фланговыми или торцевыми швами, а иногда и теми и другими вместе. Как уже указывалось, при переменных и ударных нагрузках такое «усиление» стыка может принести больше вреда, чем пользы.

Что касается расчета такого комбинированного стыка, то при одновременном применении лобовых и фланговых швов считают, что сопротивление соединения равно сумме сопротивлений всех швов, т. е. 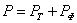, где сопротивление торцевого шва при расчетной длине 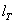равно 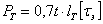, а сопротивление двух фланговых швов 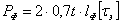, причем 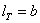, где b — ширина накладки. В результате подстановки получаем:

.

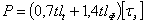Зная длину торцевого шва, определяют длину фланговых швов 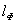.При двухсторонних накладках число швов удваивается, т. е. правую часть полученного соотношения следует удвоить.

Так как торцевые швы более жестки, то при совместной работе с фланговыми они перегружаются, что ведет к неравномерной работе соединения. Если учесть, что в таком соединении и термические напряжения достигают больших значений, то устройства такого стыка следует избегать.

Иногда при соединении внахлестку, в дополнение к фланговым швам, применяют прорезные швы, осуществляемые путем наплавки металла в узкую прорезь, сделанную в одном из соединяемых элементов параллельно действующему на соединение усилию.

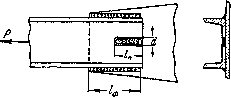
Рис.7. Комбинация фланговых и прорезных швов

При длине прорезного шва 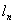и ширине прорези d сопротивление такого шва срезу равно:

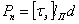
где 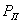— усилие, приходящееся на прорезной шов.

В комбинированном соединении с фланговыми швами для записи расчетного условия принимают, что 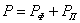или

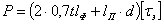
Задавшись размерами одного из швов (обычно флангового), находят необходимую длину другого. При этом ширина прорези d принимается равной двойной толщине прорезанного металла, длина — не более двадцати толщин.

Недостатками соединения с прорезными швами являются: 1) ослабление сечения прорезями вследствие неизбежного непровара и 2) высокая концентрация напряжений в основном металле в зоне сварки, ведущая к появлению трещин около углов прорезного шва; поэтому такое соединение может применяться лишь в крайних случаях, при условии хорошо продуманной технологии сварочных работ.

В заключение заметим, что в том случае, когда приходится прибегать к соединению внахлестку, лучше всего ограничиться одними фланговыми швами, избегая комбинированных соединений.

Лекция № 26. Косой изгиб призматического стержня

Вид деформации является сложным, когда в поперечном сечении стержня возникают два и более силовых факторов. Сложный вид деформации можно рассматривать как сумму простых видов, изученных ранее (растяжение, изгиб, кручение), если применим принцип независимости действия сил (частный случай принципа суперпозиции или наложения, применяемый в механике деформируемого твердого тела).

Напомним формулировку принципа независимости действия сил: напряжение (деформация) от группы сил равно сумме напряжений (деформаций) от каждой силы в отдельности. Он справедлив, если функция и аргумент связаны линейной зависимостью. В задачах механики материалов и конструкций становится неприменимым, если:

• напряжения в какой-либо части конструкции от одной из сил или группы сил превышают предел пропорциональности ;
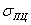• деформации или перемещения становятся настолько большими, что нарушается линейная зависимость между ними и нагрузкой.

Например, дифференциальное уравнение изгиба стержня является нелинейным и вытекающая из него зависимость прогиба f от нагрузки Р для консольной балки, изображенной на рис. 1, а, также является нелинейной (рис. 1, б). Однако, если прогибы балки невелики (f<<l) настолько, что (dv/dz)²<<1 (так как dv/dz ~ f/l), то дифференциальное уравнение изгиба становится линейным (как видно из рис. 1, б, начальный участок зависимости Р от f, описываемый этим уравнением, также является линейным).

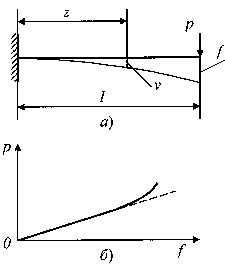
а) расчетная схема б) линейное и нелинейное сопротивления
Рис.1. Модели изгиба балки:

Известно, что косой изгиб имеет место, когда силы, его вызывающие, не лежат в одной из главных плоскостей инерции. Однако, если разложить внешние силы по главным осям инерции Ох и Оу, то получим две системы сил P_1x, P_2x, …, P_nx и P_1y, P_2y,..., P_ny, каждая из.которых вызывает прямой изгиб с изгибающими моментами соответственно M_y и М_x (рис. 2). Применяя принцип независимости действия сил, нормальные напряжения 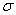(рис. 3) определим как алгебраическую сумму напряжений от M_x и М_y:

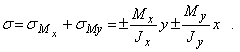
Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу. Прогибы балки определим как геометрическую сумму прогибов от прямых изгибов (рис. 2)

.

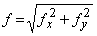Таким образом, расчет на косой изгиб с применением принципа независимости действия сил сводится к расчету на два прямых изгиба с последующим алгебраическим суммированием напряжений и геометрическим суммированием прогибов.

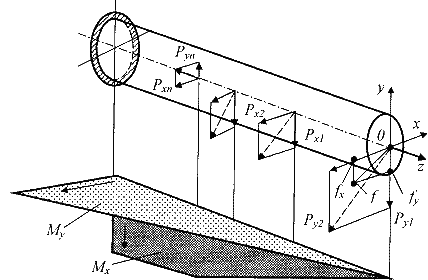
Рис.2. Расчетная модель косого изгиба бруса

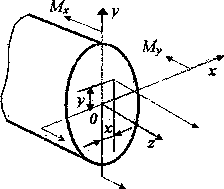
Рис.3. Связь нормального напряжения с внутренними изгибающими моментами

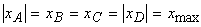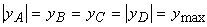В случае поперечных сечений, имеющих две оси симметрии и выступающие угловые точки (рис. 4) с равными по модулю и максимальными одноименными координатами и напряжения в этих точках будут равны

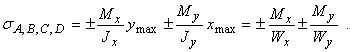
Слагаемые в этом выражении рекомендуется определять по модулю, а знаки ставить по смыслу. Например, на рис. 5 верхний ряд знаков «+» и «—» соответствует напряжениям от М_x, а нижний ряд — от M_y, и напряжения в этих точках будут равны

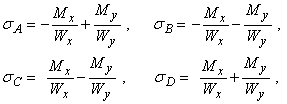
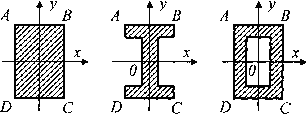
Рис.4. Симметричные варианты сечений

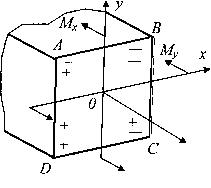
Рис.5. Расстановка знаков от действия моментов

Условие прочности для балок из пластичного материала с указанным типом сечений запишется в виде

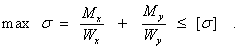
В остальных случаях для определения max а (или max dp и max 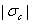для хрупкого материала) необходимо по общей формуле проверить напряжения во всех подозрительных точках.

Есть и другой путь: положив 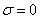, получим уравнение нейтральной линии. Так как напряжения в точках поперечного сечения будут пропорциональными расстояниям от нейтральной линии, то max 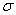будут возникать в наиболее удаленных от нее точках.

Лекция № 27. Совместное действие изгиба и растяжения или сжатия.