Побудова графіків через інтерполяцію дискретнихвідліків відрізками прямих ліній

Побудова графіка функції y=f(x) у декартовій системі координат у MatLab здійснюється дуже легко. Для виконання цієї дії використовується команда plot, яка має кілька різновидів. Найпростіша з них — це команда із двома параметрами plot(x,y), де x і y — вектора або матриці однакового розмі ру. Якщо x і y — вектора, то будується один графік, у якому значення першої змінної х відкладаються по осі абсцис, а другої змінної у — по осі ординат. Якщо х та у — матриці, то будується сукупність графіків за даними, що міститься у стовпчиках матриць. Очевидно, що явний опис функції y=f(x) не є обов’язковим. Достатньо задати два вектори — значеня аргументу та значення функції. Наприклад, графіки функцій y=sin(x) і y=cos(x) можна побудувати на одній осі координат, написавши такий фрагмент програми:

»x=0:5;

»y=[sin(x);cos(x)];

»plot(x,y)

Графік складається зі з’єднаних лінійних відрізків, як утворюють ламану лінію. Наведений приклад наочно показує побудову графіків у системі MatLab. Точки відліку відповідають цілочисловим значенням, тому за лінійної інтерполяції незначна кількість точок не дає змогу відобразити функції між відліками. Якщо ви бажаєте отримати більш гладку криву, необхідно визначити більше значень аргумента х. Результат роботи програми, яка містить команди виведення графіків, відображується в окремому графічному вікні. Скопіювати отриманий графік у буфер обміну Windows можна через команду менюEdit → Copy Figure.

Під час копіювання графіка не беруть до уваги сірий фон,на якому він розташований. Таку опцію копіювання можна задати із системного меню File → Preferences → Copying Options.

Інший формат команди plot (y), де у — вектор дійсних чисел. Буде побудований графік функції у(і), де і — номер елемента вектора. Приклад такого використання функції plot

» x=1:10

x =

1 2 3 4 5 6 7 8 9 10

» y=sin(x)

y =

Columns 1 through 7

0.8415 0.9093 0.1411 ?0.7568 ?0.9589 ?0.2794 0.6570

Columns 8 through 10

0.9894 0.4121 ?0.5440

» plot(y)

»

Якщо y— вектор комплексних чисел, команда plot(y)виконується так: plot(real(y), imag(y)). У всіх інших випадках, коли під час використання команди plot будуються графіки у дійсній площині, уявна частина даних ігнорується. Розглянемо приклад використання команди plot(y) для побудови фігури Лісажу, які є результатом накладання гармонічних коливань, що відбуваються у повздовжньому та поперечному напрямках на кратних частотах. Такі коливання описують фізичні явища утеоретичній електродинаміці та електротехніці, тому фігури Лісажу часто використовуються велектроніці під час моделювання коливальних процесів для подання остаточних результатів.

Приклад

»x=-2*pi:0.02*pi:2*pi;

»y=sin(2*x)+i*cos(3*x);

»plot(y)

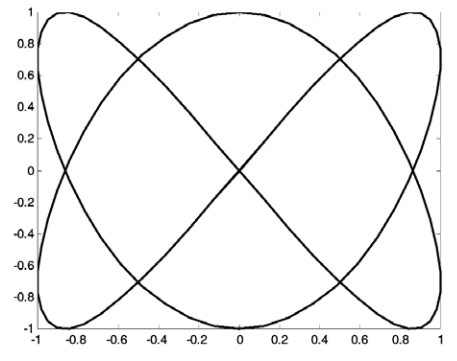
Інший спосіб побудови геометричних фігур у системі MatLab —це параметричне визначення функцій для координат х та у. Таким чином можна моделювати траєкторії часток у фізиці і механіці. Коли розподіл сил, що діють на тіло, яке рухається, має складний характер, і функція залежності координат у(х) не може бути визначена аналітично, можна побудувати траєкторію об’єкту як параметричну криву, визначену функціями y(t) та x(t), де t — час. У цьому разі використовується стандартна графічна функція plot(x, y), де х та у — вектори однакового розміру. У наступному прикладі через параметричне визначення фігура Лісажу побудована як параметрична крива.

Приклад

» t=-2*pi:0.001*pi:2*pi;

» y=sin(3*t);

» x=sin(10*t);

» plot(x,y)