Временные характеристики типовых звеньев
| Тип звена | Передаточные функции | Временные функции | |
| Позиционные звенья | |||
| Усилительное | W=K | h(t)=K×1(t) w(t)=K×d(t) | |
| Апериодическое 1-го порядка | 
| 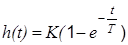 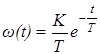
| |
| Апериодическое 2-го порядка Т1³ 2Т2 |  , , 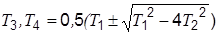
| 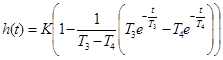 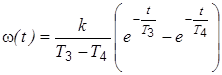
| |
| Колебательное 0<x<1 | 
| 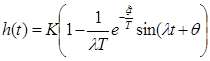 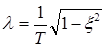 
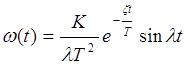
| |
| Консервативное | 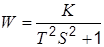
| 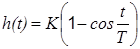 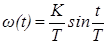
| |
| Интегрирующие звенья | ||
| Интегрирующее идеальное | 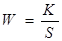
| h(t)=k× t w(t)=k×1(t) |
| Интегрирующее инерционное | 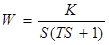
| 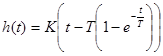 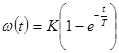
|
| Изодромное 1-го порядка | 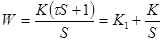 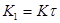
|  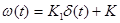
|
| Изодромное 2-го порядка | 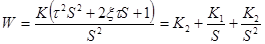 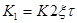 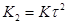
| 
|
| Дифференцирующие звенья | ||
| Идеальное дифференциру-ющее | W=KS | 
|
| Дифференциру-ющее инерционное | 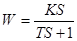
| 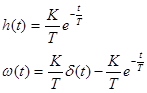
|
| Форсирующее 1-го порядка | 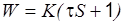
| 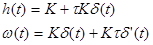
|
Частотные характеристики типовых звеньев приведены в таблице 3.3
Таблица 3.3
Частотные характеристики звеньев.
| Частотная передаточная функция | Амплитудная M(w) и фазовая j(w) характеристики | Амплитудно-фазовая частотная характеристика |
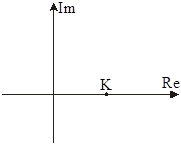 W(jw)=K W(jw)=K
| M(w)=0 j(w)=0 | |
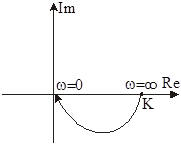 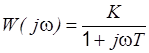
| 
| |
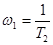 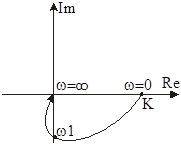 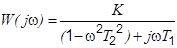
| 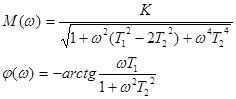
| |
 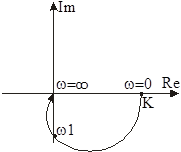 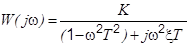
| 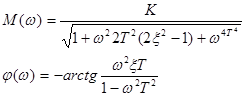
| |
 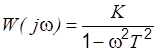
| 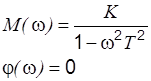
| |
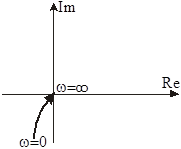 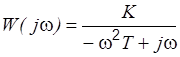
| 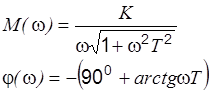
| |
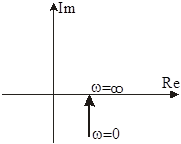 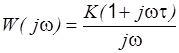
| 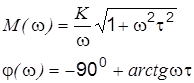
| |
 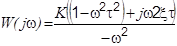
| 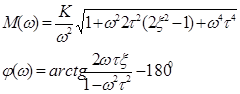
| |
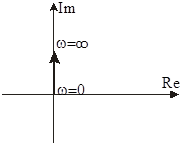 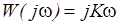
| 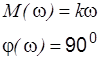
| |
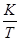 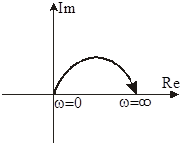 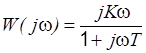
| 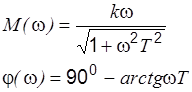
| |
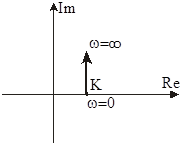 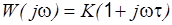
| 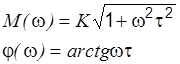
| |
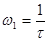 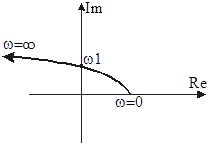 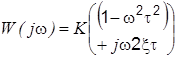
| 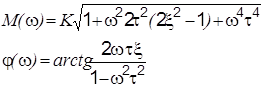
|
В табл. 3.2 и 3.3 указаны лишь характеристики основных типовых звеньев. Кроме того существуют интегро-дифференцирующие звенья и неминимально-фазовые звенья. Интегро-дифференцирующие звенья имеют передаточные функции вида
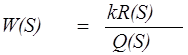 |
,
где k-постоянный коэффициент
R(S) и Q(S)- полиномы от S первого или второго порядков.
К неминимально-фазовым звеньям относятся неустойчивые звенья, передаточные функции которые имеют хотя 6ы один положительный полюс. Неминимально-фазовыми являются также звенья, которые имеют бесконечное число полюсов в левой части комплексной плоскости. Эти звенья известны под названием звенья чистого запаздывания.
Дата добавления: 2016-09-20; просмотров: 980;
