Структура и виды простых суждений

По традиции в составе простых суждений различают:

а) субъект, то есть понятие, выделяющее единичный объект или некоторое множество однотипных объектов, относительно которых что-либо утверждается либо отрицается в данном суждении; в логике это понятие называют еще субъектным термином.

б) предикат, то есть универсалия, посредством которой предметы, мыслимые в субъекте, каким-либо образом характеризуются в этом суждении; в логике такое понятие часто называют предикатным термином.

в) логическая связка между субъектом и предикатом, указывающая, что объекты, мыслимые в субъекте, имеют (или не имеют) соответствующую предикату характеристику.

Рассмотрим эти компоненты простых суждений на примерах.

1. Первый космонавт был гражданином СССР.

2. Некоторые космонавты – женщины.

3. Ни один космонавт не летал на Марс.

«О ком или о чем идет речь?» – ответ на этот вопрос позволяет установить субъект суждения. В первом суждении речь идет об одном-единственном человеке, который выделен посредством единичного понятия «первый космонавт», и это понятие является субъектом данного суждения. Второе и третье суждения имеют одинаковый субъект, который выражен общим именем «космонавт». Ответ на вопрос «Что утверждается или отрицается в отношении объектов, мыслимых в субъекте?» приводит нас к установлению предиката суждения. В первом суждении таковым является общее понятие «гражданин СССР», во втором – «женщины», в третьем – «человек, летавший на Марс».

Характеризовать – значит утверждать наличие либо отсутствие какого-то свойства у некоторого объекта (или объектов). В русском языке это можно сделать посредством логической связки «есть» (или «суть»), соответственно, сочетания «есть» с частицей «не» («не есть», «не суть»). Вместо слова «есть» употребляются нередко тире «–», слово «является», словосочетание «представляет собой» и т.п. Слова-связки могут употребляться не только в настоящем времени, но и в прошедшем (к примеру, «был») или будущем («будет»). Нередко связка вообще не фигурирует в явном виде, как это имеет место во втором суждении, однако сама логическая связь между субъектом и предикатом при этом не утрачивается. Предикат в суждениях 1. и 2. представлен общими именами «гражданин СССР» и «женщина». Однако так бывает не всегда. В частности, в суждении 3. к предикату относится неполное в грамматическом отношении выражение «летал на Марс». В таких случаях полезно восполнять грамматическую структуру предиката до соответствующей понятийной знаковой формы (в нашем случае эта структура примет вид выражения «человек, который летал на Марс»).

Из примеров 1.-3. нетрудно усмотреть, что по характеру субъектов простые суждения делятся на единичные (первое суждение) и множественные (второе и третье суждения). В единичном суждении его субъект представлен единичным понятием, во множественном – общим. Во множественных суждениях, наряду с субъектом, предикатом и связкой, имеются также кванторные слова – «все» (т.е. «каждый», «любой», «всякий»), «некоторые» (т.е. «существуют», «иные», «многие», «большинство», «по меньшей мере, один»). Кванторы указывают, относится ли утверждение или отрицание ко всем выделяемым субъектом объектов, или только к части соответствующего множества.

Простые суждения обычно называют категорическими, подчеркивая тем самым их отличие от сложных суждений, содержащих логические союзы «если, то», «или», «и» и др. В формулировке категорических суждений кванторное слово иногда опускается, как это имеет место в предложении «Металлы являются хорошими проводниками электрического тока». Однако содержащееся в нем утверждение относится ко всем металлам, а не к их части (т.е. к некоторым металлам) и не к одному какому-то (определенному) металлу.

Отношения между субъектом и предикатом простого суждения можно также истолковать как отношение включения (или невключения) одного множества объектов (например, множества адвокатов), в другое множество (во множество юристов), или единичного объекта (например, Ю.А. Гагарина) в некоторое множество (например, граждан СССР).

С учетом изложенного все простые суждения мы будем подразделять по двум основаниям:

· по качеству –на утвердительные и отрицательные;

· по количеству –на единичные, частные и общие.

Суждение 1. является по качеству утвердительным, по количеству – единичным (а в целом – единичноутвердительным); суждение 2. – утвердительным и частным (частноутвердительным); суждение 3. – отрицательным и общим (общеотрицательным).

Логику как науку иногда называют формальной логикой: те законы, принципы и правила, которые устанавливает данная наука, относятся не к конкретному содержанию наших понятий и суждений, а к их предельно общей структуре – логической форме. Логическую форму суждений в данном аспекте мы будем истолковывать как способ связи их основных частей (компонентов). В простых суждениях к этим частям относятся их субъекты и предикаты, а способ их связи представлен логическими связками и кванторными словами. Для краткой записи логической формы категорических суждений воспользуемся заглавными буквами латинского алфавита S, Р, Q и т.д. Эти символы (параметры) указывают только на логическую категорию

соответствующих им выражений естественного языка, посредством чего происходит абстрагирование (отвлечение) от того, какие конкретно свойства и соответствующие им множества предметов они представляют. Рассмотрим следующую таблицу:

Названия видов категорических суждений	Логические формы суждений	Отношения терминов (S и P)	Распределенность терминов
Общеутвердительные (Сокращенно: суждения типа а)	Все S есть P (Сокращенно: SaP)		Р   S+
Общеотрицательные (суждения типа е)	Все S не есть P (SeP)		Р+ S+
Частноутвердительные (суждения типа i)	Некоторые S есть P (SiP)		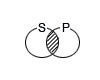Р S
Частноотрицательные (суждения типа о)	Некоторые S не есть P (SoP)		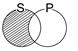Р+ S

Логическая форма общеутвердительных суждений представлена в этой таблице в виде формулы «Все S есть P» (см. второй столбец), смысл которой иллюстрирует отношение объемов субъектного термина S и предикатного термина P (см. третий столбец): их объемы находятся в отношении логического подчинения субъекта предикатом. Это, в свою очередь, означает (см. четвертый столбец), что в общеутвердительном суждении субъект S распределен (это обстоятельство будем отмечать символом ⁺), то есть имеется полная определенность относительно элементов объема этого понятия: любой из них входит в объем предиката P. Предикат же общеутвердительного суждения не распределен (это обстоятельство будем отмечать символом ^), поскольку не исключен вариант, когда некоторые элементы объема термина P не входят в объем термина S (что хорошо видно на соответствующей схеме, см. третий столбец).

В общеотрицательном суждении речь идет о каждом элементе объема S в том смысле, что любой из них не входит в объем P; в отношении элементов P такая же картина: ни один из них не входит в объем S. Поэтому в этом виде суждений распределен и субъект (S ⁺), и предикат (P ⁺).

В частных суждениях нет определенности в отношении их субъектов: на основании их логических форм известно только, что некоторые из элементов их объемов (т.е. по меньшей мере, один, хотя не исключено, что и больше) включаются в объем предиката, либо не входят в него. Поэтому субъекты этих суждений не распределены (S^–). В частноутвердительном суждении не распределен также предикат (P^–), а в частноотрицательном предикат распределен (P⁺).

Вообще же вопрос о распределенности терминов в категорических суждениях решается просто:вобщихсуждениях всегда распределен субъект (S ⁺),а в отрицательныхвсегда распределен предикат (P⁺).

В число простых входят и единичные суждения. Вопрос о распределенности их терминов решается следующим образом: субъект в них распределен; предикат распределен в единичноотрицательном и не распределен в единичноутвердительном. Поскольку в обоих этих суждениях распределен субъект, а в единичноотрицательном суждении распределен и предикат, будем в дальнейшем полагать, что логическая формула единичноутвердительного суждения совпадает с формой общеутвердительного, а единичноотрицательного – с формой общеотрицательного.

Практикум

1. Выделите субъект в следующих суждениях:

1) Бутылка «Пепси-колы» стоит сорок центов. 2) Некоторые имена существительные не изменяются по падежам. 3) Цицерон великолепно владел латинским языком. 4) Иные хорошие книги так и остаются непрочитанными. 5) Кто ищет, тот всегда найдет.

2. Найдите предикаты в следующих суждениях. Определите, являются эти суждения утвердительными или отрицательными:

а) Этот город не больше поселка. б) Некоторым современным британцам читать Шекспира нелегко. в) Ни в одной книге нет столько ошибок, сколько в этой. г) Нет семиклассника, которому неизвестна теорема Пифагора.

3. Определите, какие из приведенных ниже суждений являются единичными, какие – общими, а какие – частными:

1) Некоторые ромбы одновременно представляют собой квадраты. 2) Ни один истинный мусульманин не станет пить вина. 3) Млечный путь хорошо виден в декабре. 4) Большинство политиков в принципе неплохие люди.
5) Рейкьявик – самая северная столица мира.

4. Найдите квантор, субъект и предикат, выделите связку, определите логический тип категорических суждений:

Кое-какие книги о путешествии Колумба были в школьной библиотеке. Любая работа, в которой нет новых идей, не достойна премии. Некоторые современники динозавров не вымерли до сих пор. Вокруг некоторых коммерческих структур формируется криминогенная среда. Ни одно государство не обходится без армии.

*Пример: Все стрелки, не сделавшие ни одного промаха, были \включены в команду. Квантор – «все» (общности), связка – «суть», субъект – «стрелки, не сделавшие ни одного промаха», предикат – «спортсмены, включенные в команду». Таким образом, суждение общеутвердительное: Все S суть P.

5. Определите тип категорических суждений, приведите их к стандартной форме, покажите распределенность терминов на круговых схемах.

1. По некоторым делам предусматривается законом проведение экспертиз. 2. Лицо, виновное в совершении преступления, подлежит уголовной ответственности. 3. «Дни поздней осени бранят обыкновенно». (А.С. Пушкин)

*Чтобы определить распределенность терминов в категорическом суждении, необходимо привести его к стандартной форме: Все (Некоторые) S суть (не суть) Р. Лишь после этого, выделив кванторное слово, термины S и Р, следует перейти к иллюстрации их объемных отношений на круговых схемах. Пример: Каждое государство Восточной Европы – республика. Связка явно не выражена, ее можно восстановить: это будет утвердительная связка – «является» («суть»); квантор этого суждения – «каждый» (квантор общности). Таким образом, получаем общеутвердительное суждение. Субъектом его является понятие «государство Восточной Европы» (S), а предикатом – понятие «республика» (Р). Логическая форма суждения: Все S суть Р. Отношение между объемами S и Р этого суждения будет следующим: объем термина S полностью включен в объем термина Р, следовательно, термин S распределен (S ⁺), термин же Р частично включен в S, а частично исключен из него, значит, он не распределен (P ^–).

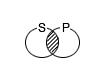
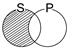
6. Составьте суждения с указанными субъектом и предикатом так, чтобы их отношения соответствовали приведенным ниже схемам; отметьте, какие из полученных суждений истинны, а какие ложны:

S – россиянин, Р – космонавт.

7. Подберите истинные суждения с заданной ниже распределенностью терминов:

а) S ^-, Р⁺; б) S ⁺, Р⁺; в) S ^-, Р^-; г) S ⁺, Р^-

8. Распределен ли субъект в следующих суждениях?

1. Все счастливые семьи счастливы одинаково. 2. Субъект общего суждения распределен. 3. Каждая несчастливая семья несчастлива по-своему. 4. Некоторые солдаты не мечтают стать генералами.

9. Распределен ли предикат в следующих суждениях?

1. Ни один студент не является лауреатом Нобелевской премии.
2. Некоторые законы физики по своему характеру являются статистическими. 3. Все имена существительные изменяются по падежам.