Связь между утверждением и отрицанием
Как уже ранее отмечалось, суждение является либо истинным – когда то, о чем в нем «говорится», имеет место в действительности, либо ложным – когда действительность не совпадает с тем, о чем повествуется в этом суждении. Когда суждение истинно, оно составляет частицу нашего знания о мире, и тем самым помогает нам ориентироваться в нем. Спрашивается, может ли быть полезным ложное (в смысле – неистинного) суждение? Может, но при одном условии: если нам известно, что оно ложное. Из такого суждения мы, возможно, немногое узнаем о мире, но все-таки что-то узнаем, а именно: мир не таков, каким он предстает в данном суждении. Познавательную ценность ложным суждениям придает логическая операция отрицания. В обычном языке отрицание может выражаться такими словами как, «неверно, что» или частицей «не». Естественно, прежде чем суждение (как мысль о чем-то) может быть подвергнуто отрицанию, оно должно быть высказано как утверждение.
Полезно различать отрицание внешнее и внутреннее отрицание. С внутренним отрицанием мы уже знакомы: оно входит в состав общеотрицательных и частноотрицательных суждений. Теперь введем понятие внешнего отрицания: оно помещается перед высказыванием, а связь между суждением и результатом его логического отрицания воспроизводится нижеследующей таблицей истинности:
| Х | Неверно, что Х | ┐Х |
| И | Λ | Λ |
| Л | И | И |
где символ ┐ обозначает выражение «неверно, что», или частицу «не» перед суждением (не-Х). Из таблицы хорошо видно, что когда Х является истинным суждением, то ┐Х становится ложным; когда Х является ложным суждением, то ┐Х становится истинным. Например, суждение «Киев расположен на берегу Днепра» – истинное, а результат его отрицания – «Неверно, что Киев расположен на берегу Днепра» – ложное суждение. Аналогично, суждение «Все юристы – высококлассные специалисты» – ложное, а его отрицание «Неверно, что все юристы – высококлассные специалисты» – истинно.
Сформулируем теперь эквивалентности, позволяющие перенести отрицание, стоящее перед категорическим суждением, во внутреннюю его структуру, либо устранить его вовсе:
(1)┐(Все S суть P) ≡ Некоторые S не суть P.
(2)┐(Все S не суть P) ≡ Некоторые S суть P
(3)┐(Некоторые S суть P) ≡ Все S не суть P
(4)┐(Некоторые S не суть P) ≡ Все S суть P
Символ ≡ прочитывается как «логически равнозначно», или «эквивалентно». Данные эквивалентности можно сформулировать так: логический эквивалент категорического суждения с внешним отрицанием (правая сторона) получается заменой кванторных слов на противоположные («Все» на «Некоторые», и наоборот), и, одновременно, изменением качества отрицаемого суждения. Рассмотрим суждение Неверно, что некоторым людям нравится болеть. Логическая форма этого суждения такова:
Неверно, что (Некоторые S суть P)
где S замещает понятие «люди», а Р – «те, которым нравится болеть». Следуя только что сформулированному общему правилу, получаем:
Все S не суть P,
что в данном конкретном случае означает: Ни одному человеку не нравится болеть.
Практикум
1. Определите, из каких простых суждений составлены следующие сложные.
1. Январь и февраль – зимние месяцы. 2. Болгария расположена в Европе и является республикой. 3. Тела от холода сжимаются, а от тепла – расширяются. 4. «Если с другом вышел в путь – веселей дорога» (из песни). 5. Греки любили поболтать, зато и первыми начали философствовать.
2. Определите вид и логическую форму, запишите с помощью символики следующие сложные суждения:
1) Если самолёт терпит аварию, то летчик либо катапультирует, либо пытается c риском для жизни посадить машину.
2) Если бы Иван IV был зол по природе и не заботился об интересах государства, то он не отменил бы опричнины.
3) Если вода из естественных, либо из искусственных водоемов по показаниям анализов стала малопригодной для питья и приносит некоторый вред, санэпидстанция обязана принять срочные меры по оздоровлению источников.
4) Никто не может подвергаться произвольному вмешательству в его личную и семейную жизнь, произвольным посягательствам на неприкосновенность его жилища, тайну его корреспонденции или на его честь и репутацию.
5) Неверно, что Петров – чемпион по прыжкам в высоту и высок ростом.
*Рассмотрим пример: Если однородные члены предложения стоят между подлежащим и сказуемым, причем этим однородным членам предшествует обобщающее слово, то перед однородными членами ставится двоеточие, а после них – тире. Данное суждение является сложным, в нем можно выделить четыре простых. Обозначим каждое простое суждение логическим символом:
x – Однородные члены предложения стоят между подлежащим и сказуемым;
y – Обобщающее слово предшествует однородным членам предложения;
z – Двоеточие ставится перед однородными членами;
f – Тире ставится после однородных членов предложения.
Первые два суждения выражают некоторое условие (наличие которого требует соответствующих действий) и объединены конъюнктивной связью, то есть образуют соединительное суждение, имеющего логическую форму «x и y». Суждения же z и f выражают, в совокупности, требуемое действие: «z и f». Таким образом, логическая формула рассматриваемого суждения имеет вид выражения (импликативной) формулы:
Если имеют место ситуации x и y, то имеют место ситуации z и f
Логическая форма рассматриваемого суждения, выраженная на языке символов, имеет вид импликативной формулы:
(xÙy) ® (zÙf).
3. Переведите на логический язык сложных суждений следующие высказывания:
а) «Иль чума меня подцепит, иль мороз окостенит / Иль мне в лоб шлагбаум влепит непроворный инвалид» (А. Пушкин). б) Если сдам сегодня экзамен, то завтра поеду в деревню к деду. в) «Бывают роковые дни лютейшего телесного недуга / И страшных нравственных забот» (Ф. Тютчев).
г) Если у берега много медуз, то был шторм или вода в море остыла.
4. Определите логическую форму сложных суждений и установите их вид (по главному логическому союзу):
а) Если человек читал книгу, то знает ее содержание или основную идею. б) Неверно, что Иванов не учился ни в вузе, ни в техникуме.
в) Он не был ни прилежным, ни способным. г) На этом факультете учатся только способные студенты. д) Н. не будет получать стипендию, разве что сдаст экзамен до завтра. е) «Когда в товарищах согласья нет, на лад их дело не пойдет» (И.А. Крылов). ж) Пойдешь налево – коня потеряешь, а не пойдешь – сам погибнешь. з) Я никогда не решился бы на это, не будь его рядом.
3.6. Модальные суждения
и логические отношения между ними
До сих пор речь шла только об ассерторических суждениях,т.е. таких, в которых утверждается наличие либо отсутствие некоторой ситуации (присущность какого-либо свойства предметам, нахождение их в определенных отношениях и т.п.). Однако мыслимая в ассерторическом суждении ситуация наличествует (или отсутствует) в действительности либо случайно, либо необходимо, она возможна (в будущем), или невозможна. Аналогично, поступки, действия людей, воспроизводимые ассерторическими суждениями, могут быть в обществе либо разрешены, либо запрещены, либо обязательны. Наконец, ассерторические суждения о мире могут быть доказаны или опровергнуты, либо никому не удалось сделать ни того, ни другого. Суждения, в которых содержатся подобные характеристики, или оценки ситуаций, действий и знаний, называются модальными. Слова, с помощью которых фиксируется модальность суждения (типа «необходимо», «разрешено», «доказано» и т.п.), называются модальными функторами, или понятиями.
Среди известных модальностей выделяют:
1) Алетические, выражаемые функторами «необходимо», «возможно», «случайно».
2) Деонтические (от греч. deonte – как должно быть) – характеристики действий и поступков людей в обществе типа «обязательно», «разрешено», «запрещено».
3) Эпистемические (от греч. episteme – знание) – оценки наших знаний вида «доказано», «опровергнуто», «проблематично» (в смысле «не исключено, что истинно»).
Некоторые свойства приведенных модальностей могут быть уточнены путем определения логических отношений между содержащими эти функторы суждений. Пусть символ x представляет какое-то событие, некоторую ситуацию или определенный процесс. Тогда логические формы алетических модальностей будут представлены выражениями Необходимо, что x; Возможно, что х; Случайно, что х. Имеют место следующие эквивалентности между алетическими модальностями:
1. Необходимо, что xравнозначноНеверно, что возможно не-x
2. Случайно, что xравнозначноВозможно, что x и возможно,
что не- x
3. Неверно, что необходимо xравнозначноВозможно, что не-x
4. Возможно, что х равнозначноНеверно, что необходимо не-x
Рассмотрим пример. Известна истина Все живое – смертно. Это суждение может являться не только результатом обобщения многочисленных фактов, но и выражать некий биологический закон, природную необходимость. Поэтому его можно сформулировать как суждение алетической модальности Необходимо, что любое живое существо смертно. Этому суждению в соответствии с эквивалентностью 1. равнозначно суждение Неверно, что возможно так, что некоторые живые существа не являются смертными.
Суждения с алетическими модальностями оцениваются как истинные либо ложные.
Суждения с деонтическими модальностями выражают некоторые нормы. Нормы определяют, что должен (обязан) делать тот-то и тот, что и кому разрешено (запрещено). Логические формы деонтических суждений таковы: Обязательно, что x; Разрешено, что x; Запрещено, что x; Неверно, что разрешено не-х и т.п. В отношении деонтических модальностей справедливы такие эквивалентности:
1. Неверно, что запрещено xравнозначноРазрешено, что x
2. Обязательно, что x равнозначноНеверно, что разрешено не-x
3. Запрещено, что xравнозначно Обязательно, что не-x
Рассмотрим суждение Преступление уголовно наказуемо. Оно не столько описывает фактическое положение дел в обществе, сколько устанавливает некую норму-требование Любое преступление подлежит соразмерному уголовному наказанию. Отсюда видно, что анализируемое суждение содержит деонтическую модальность и может быть представлено формулой Обязательно, что x, где x – суждение Любое преступление уголовно наказуемо. Используя эквивалентность 2., получаем равнозначное исходному суждение Не разрешено так, что некоторые преступления не являются уголовно наказуемыми.
Синтаксически (грамматически) деонтические суждения могут быть выражены в форме ассерторических суждений. К примеру, в суждении Приговор выносится именем Российской Федерации формулируется, по сути дела, соответствующая правообязывающая норма, а не констатация некоторого факта.
Правовые нормы можно оценивать в качестве нормативно-истинных или нормативно-ложных, если они соответствуют либо не соответствуют целям, которые ставит законодатель, выражая свою волю.
* * *
Как мы помним, заблуждается тот, кто признает за истину и некоторое суждение, и его отрицание. Речь идет о законе противоречия:
Неверно, что Х и не-Х
Полезно обратить внимание на формулировку этого закона применительно к суждениям с деонтической модальностью. Вот некоторые из них:
1. Неверно, что обязательно x и разрешено не- x
2. Неверно, что разрешено x и запрещено x
На языке правовых норм логическую форму 1. имеет, к примеру, суждение Неверно, что каждый работающий гражданин обязан платить налоги и в тоже время некоторые из работающих граждан могут налоги не платить, а форму 2. – суждение Неверно, что всем гражданам, достигшим 18 лет, разрешено участвовать в выборах, но некоторым из них это запрещено.
В законодательствах, уставах и договорах нередко встречаются логически противоречивые («конфликтующие») нормы, когда одна из них что-то запрещает, а другая это же самое разрешает, одна обязывает к какому-либо действию, а другая разрешает не совершать его. Такие деонтически противоречивые документы приводят к конфликтам между людьми, организациями и странами, в которых виноваты не столько они сами, сколько юристы, которые принимали участие в их составлении. К примеру, в Конвенции ООН по морскому праву (UNCLOS), определяющей особенности судоходства в покрытых льдами районах говорится, с одной стороны, о недискриминационном транзите судов третьих стран, а с другой –
о праве прибрежных государств определять собственные стандарты.
Всем людям, находящимся в здравом уме, логика не рекомендует также нарушать закон исключенного третьего:
Х или не-Х
Приведем некоторые формулировки этого закона на языке деонтических модальностей:
1. Обязательно x или разрешено не-x
2. Разрешено x или запрещено x
На языке правовых норм логическую форму 1. имеет, к примеру, суждение Каждый гражданин РФ мужского пола, которому исполнилось
18 лет, обязан пройти службу в рядах российских вооруженных сил (если нет противопоказаний к ней), или некоторым из них (при этом же условии) разрешено не служить в армии, а форму 2. – суждение Всем гражданам, достигшим возраста 18 лет, разрешено участие в выборах или некоторые из них лишены такого права.
Желательно, чтобы любая социально-значимая деятельность физического лица или организации имела правовую квалификацию в терминах деонтических модальностей. Однако нередко бывает так, что система правовых норм неполна, т.е. в ней прописаны законодателем правовые нормы не для всех видов социально-значимой деятельности или не для всех категорий правоответственных граждан. В этих случаях трудно решить, к примеру, обязан ли гражданин делать то-то и то-то в таких-то и таких обстоятельствах, или ему разрешено не делать этого.
Логические формы эпистемических модальностей представим выражениями: Доказано, что x; Проблематично, что x; Опровергнуто, что x. В отношении этих модальностей имеем следующие логические зависимости:
1. Доказано, что xравнозначноНеверно, что проблематично
не-x
2. Доказано, что не-xравнозначноОпровергнуто, что x
3. Проблематично, что xравнозначноНеверно, что доказано x, и
неверно, что опровергнуто x
4. Еслидоказано, что х,тох истинно
5.Еслиопровергнуто, что х,то х ложно
К примеру, доказать, что подсудимый виновен – значит исключить возможность его невиновности, и обратно (согл. экв. 1). Если доказано, что подсудимый невиновен, то это означает, что опровергнуто обвинение против него; опровергнуть обвинение – значит доказать невиновность подсудимого (согл. экв. 2). Если не доказана виновность и она не опровергнута, следует считать, что виновность (либо невиновность) подсудимого не исключена, и обратно (согл. экв. 3). Если доказана виновность подсудимого, то следует полагать, что он совершил это преступление (согл. экв. 4); обратное верно не всегда. Если опровергнута виновность, то следует полагать, что подсудимый является невиновным (согл. экв. 5); обратное верно не всегда.
(Логическая суть доказывания и опровержения специально будет рассматриваться в разделах 5.3.1 и 5.3.2.).
Практикум
1. Определите вид модальности (выделите модальное понятие) следующих суждений; представьте логические формы этих суждений:
1) Невозможно без весел плыть против течения. 2) Проблематично, что существует творящее Мир начало. 3) Любой гражданин обязан соблюдать законы государства. 4) Доказано, что Земля вращается вокруг Солнца. 5) Необходимо, что Земля вращается вокруг своей оси.
*Выполним задание в отношении суждения Не доказано и не опровергнуто, что Бог существует. Это суждение относится к эпистемическим модальным суждениям, поскольку в нем фигурируют модальные функторы доказано и опровергнуто. Основу этого суждения составляет ассерторическое суждение Бог существует, которое мы заменяем параметром х. Строим формулу этого суждения: Не доказано, что х, и не опровергнуто, что х
2. Следующие деонтические модальные суждения выразите в символической форме:
1) Запрещается изменение стоимости утвержденных проектов за счет исключения планируемых мероприятий по охране окружающей среды.
2) Строительство зданий должно осуществляться по утвержденным проектам, имеющим положительные заключения государственной экологической экспертизы.
3) Деятельность, осуществляемая с нарушением природоохранных требований, может быть прекращена в порядке, установленном законодательством Российской Федерации.
4) При осуществлении строительства зданий принимаются меры по охране окружающей среды в соответствии с законодательством Российской Федерации.
5) Проекты, по которым не имеются положительные заключения государственной экологической экспертизы, утверждению не подлежат.
3. Сформулируйте суждения, эквивалентные приведенным в упр. 2., заменяя модальные функторы в соответствии с зависимостями: Запрещено, что x равнозначно Обязательно, что не-x; Обязательно, что x равнозначно Неверно, что разрешено не-x; Разрешено x равнозначно Неверно, что запрещено x.
*Выполним задание в отношении суждения Государственные инспектора в области охраны окружающей среды обязаны соблюдать требования законодательства. Заменим параметром х утверждение Государственные инспектора в области охраны окружающей среды соблюдают требования законодательства. Тогда анализируемое суждение в логической символике примет вид формулы Обязательно, что х. Поскольку Обязательно, что x равнозначно Неверно, что разрешено не-x, получаем: Неверно, что государственным инспекторам разрешено не считаться с требованиями законодательства.
4. Сформулируйте на основе суждений, приведенных в упр.2., противоречащие им суждения.
*Выполним задание в отношении суждения Все граждане обязаны бережно относиться к природе, логической формой которого является выражение Обязательно, что х. В соответствии с формулой закона противоречия Неверно, что обязательно x и разрешено не- xпротиворечить данному суждению будет суждение Разрешено некоторым гражданам не относиться рачительно к природе.
5.Имея в виду зависимости 1.-5. между эпистемическими модальностями, ответьте на следующие вопросы:
1) Равнозначны ли суждения Доказано, что инспектор N. нарушил законодательство и Суждение о том, что инспектор N. нарушил законодательство – истинно? 2) Равнозначны ли суждения Опровергнуто, что инспектор N. нарушил законодательство и То, что инспектор N. нарушил законодательство – ложно? 3) Следует ли из того факта, что Инспектор N. нарушил законодательство, утверждение Доказано, что инспектор N. нарушил законодательство? 4) Равнозначны ли суждения Доказано, что инспектор N. нарушил законодательство и Неверно, что суждение «Инспектор N. не нарушил законодательства» проблематично?
Тема 4.УМОЗАКЛЮЧЕНИЕ

4.1. Назначение, структура
и основные виды умозаключений
Высказывая некоторое суждение, мы считаем его либо истинным, либо более или менее правдоподобным. В первом случае будем говорить, что данное суждение признается со всей определенностью, а во втором – с некоторой степенью определенности. «Суждение признается со всей определенностью» означает то же, что и «имеется доказательство истинности этого суждения». «Суждение признается с некоторой степенью определенности» означает то же, что и «Имеются некоторые доводы в пользу истинности этого суждения, но отсутствует его доказательство». Естественно, что признание кем-либо некоторого суждения с некоторой степенью определенности отнюдь не означает, что это суждение объективно является истинным.
Основания, по которым признается некоторое суждение, могут быть разными. В одних случаях таким основанием является наблюдение, непосредственное восприятие какого-либо положения вещей или некоторой ситуации. Например, к признанию со всей определенностью суждения На моих часах половина первого склоняет наблюдение, т.е. непосредственное восприятие мною положения стрелок на циферблате часов. А когда я ищу ответ на вопрос, делится ли число 1569 на 3, утвердительный ответ я могу получить на основе суждения Если сумма цифр некоторого числа делится на 3, то и само это число делится на 3, истинность которого мне заранее известна, и суждения Сумма цифр этого числа делится на 3. Другими словами, искомый ответ я нахожу посредством следующего умозаключения:
1. Если сумма цифр некоторого числа делится на 3,
то и само число делится на 3.
 2. Сумма цифр числа 1569 делится на 3
2. Сумма цифр числа 1569 делится на 3
 3. Число 1569 делится на 3.
3. Число 1569 делится на 3.
Вы уже знаете, что суждения 1. и 2., признание которых склоняет к признанию суждения 3., в логике называют посылками,а суждение 3., признаваемое на основе суждений 1. и 2., именуют заключением. Мыслительный процесс, в котором на основе признания посылок осуществляется переход к признанию заключения, называют умозаключением. Черта, отделяющая заключение от посылок, прочитывается в этой записи как «следовательно» («значит», «в силу этого»).
Умозаключение не является суждением (хотя и формируется из суждений), и потому не может характеризоваться как истинное либо ложное: таковыми могут быть только посылки или заключение. Не любой переход от признания одних суждений к признанию другого является логически безупречным (правильным, или корректным): необходимо, чтобы заключение выводилось из посылок по правилам логики. Так, не является правильным умозаключением последовательность истинных суждений:
Все судьи имеют высшее юридическое образование.
Иванов П.К. – женатый мужчина.
 Иванов П.К. увлекается классической музыкой.
Иванов П.К. увлекается классической музыкой.
Черта, отделяющая посылки от заключения и символизирующая обоснованность заключения этими посылками, здесь вообще не уместна. А вот ранее приведенная последовательность суждений является правильным умозаключением, равно как и нижеследующая:
Все адвокаты имеют высшее юридическое образование.
 Иванов П.К. – адвокат.
Иванов П.К. – адвокат.
 Иванов П.К. имеет высшее юридическое образование.
Иванов П.К. имеет высшее юридическое образование.
В любом корректном умозаключении признание посылок побуждает нас к признанию заключения, что обусловлено истинностью его посылок и его логической правильностью. Различают логические правила двух видов: дедуктивные, гарантирующее истинность заключения при истинности посылок, и индуктивные, обеспечивающее при этих же условиях лишь повышение степени правдоподобия заключения (вероятности его истинности). Соответственно, умозаключения, в которых из посылок заключение выводится по дедуктивным правилам, называются дедуктивными, а если по индуктивным правилам – именуются индуктивными.
1. Правильность дедуктивных умозаключений не зависит от конкретного содержания входящих в них суждений. Она зависит только от логической формы этих суждений, т.е. способа связи терминов по объему в простых суждениях и смыслом логических союзов в сложных суждениях. Покажем это на примере:
(I) 1. Преступление – наказуемо.
2. Дача взятки – преступление.
 3. Дача взятки – наказуема.
3. Дача взятки – наказуема.
Отвлечемся от содержания дескриптивных терминов, входящих в состав посылок и заключения, заменив слово «преступление» параметром М, слово «наказуемо» (т.е. выражение «наказуемое деяние») – параметром Р, выражение «дача взятки» – параметром S. Введем количественные характеристики суждений, составляющих посылки и заключение, а также слово «суть», указывающее на включение одного множества предметов в другое, более широкое. Получаем:
(II) 1. Все М суть Р
 2. Все S суть М
2. Все S суть М
 3. Все S суть Р
3. Все S суть Р
Данная структура называется формальной схемой умозаключения (I), поскольку входящие в него знаковые структуры 1.-3. являются уже не суждениями, а логическими формами (или формулами) этих суждений. Если теперь в этой схеме подставить на места М, Р и S другие (попарно различные) дескриптивные термины, мы вновь получим умозаключение, в котором при истинности посылок заключение с «железной» необходимостью также будет истинным. Приведем еще два примера умозаключений по схеме (II):
1. Растения (М) обогащают воздух кислородом (Р)
2. 
 Деревья (S) – растения (М)
Деревья (S) – растения (М)
3. Деревья (S) обогащают воздух кислородом (Р)
1. Преступление (М) – общественно опасное деяние (Р)
2. Получение взятки (S) – преступление(М)

 3. Получение взятки (S) – общественно опасное деяние (Р)
3. Получение взятки (S) – общественно опасное деяние (Р)
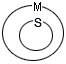
Причина, по которой эти умозаключения оказываются корректными, заключена в соотношений объемов их терминов, подставляемых на места параметров М, Р и S в формальной схеме вывода (II):
| 1. Все М суть Р: | 2. Все S суть М: |
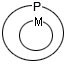
| 
|
Совместив эти две круговые схемы в одну, получаем:
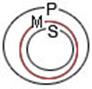
Теперь наглядно убеждаемся, что при истинности любых по конкретному содержанию суждений-посылок, имеющих логическую форму «Все М есть Р» и «Все S есть М», обязательно истинным будет и суждение формы «Все S есть Р».
Полезно сопоставить алгебраическое уравнение а + b = b + aсо схемой дедуктивного умозаключения. Как известно, это алгебраическое равенство сохраняется при любых конкретных числовых значениях переменных а и b: 4+3 =3+4, 5+6 = 6+5, и т.п. Аналогично, связь логических форм посылок с логической формой заключения в дедуктивных умозаключениях не зависит от конкретного содержания входящих в них суждений.
2.Достоверные (истинные) посылки индуктивного умозаключения обеспечивают лишь большую степень правдоподобия суждения, являющегося заключением, по сравнению с той, которую имело это суждение без учета посылок. Слыша гром и памятуя о том, что после удара молнии всегда раздается гром, мы индуктивно заключаем, что где-то был удар молнии. Однако гром мог иметь и иную причину (например, пушечный выстрел). Для индуктивных умозаключений как раз и характерна опора не только на логическую форму входящих суждений, но и на некоторые неформальные (содержательные) моменты (в нашем примере: «В мирное время пушки стреляют крайне редко»).
Следует сразу же отметить, что индуктивные умозаключения играют в мышлении ничуть не меньшую роль, чем дедуктивные. Если дедуктивные умозаключения позволяют систематизировать уже имеющееся знание, устанавливать логические связи «внутри» этого знания, применять общее знание к конкретным ситуациям, то индуктивные умозаключения участвуют при создании и обосновании гипотез, формировании нового знания. Возникает вопрос, как установить, что они выполняют эти функции? Наиболее простой способ состоит в следующем: если заключение получено из посылок по установленным наукой логикой правилам (логическим правилам), тогда такое умозаключение является корректным. В противном случае оно не является корректным. Правила эти таковы, что в дедуктивных выводах они гарантируют получение из истинных посылок истинного заключения, а в индуктивных – повышение степени правдоподобия суждения, являющегося заключением.
Практикум
1. Выделите посылки и заключение следующих умозаключений, запишите их в «столбик»: сначала посылки одну под другой, затем, отделив их чертой, заключение.
а) Мошенничество наказуемо, поскольку мошенничество – преступление, а любое преступление наказуемо.
б) Когда в мае идут дожди, жди хорошего урожая ржи:в позапрошлом году май был дождливым, а потом был хороший урожай ржи; в прошлом году май тоже был дождливым, и рожь тоже уродилась на славу.
в) Если Фред убил Джона, то он знает обстоятельства его смерти. Фреду известны обстоятельства смерти Джона. Следовательно, Фред убил Джона.
г) Все квадраты – равносторонние прямоугольники, следовательно, некоторые равносторонние прямоугольники – квадраты.
*Пример: Рассмотрим следующее умозаключение: Все дети любят мультфильмы. Значит, некоторые школьники любят мультфильмы, так как некоторые дети – школьники. На то, что эта последовательность суждений является умозаключением, указывает слово «значит» (т.е. «следовательно» или «поэтому»). Естественно полагать, что за этим словом располагается заключение – суждение Некоторые школьники любят мультфильмы. Суждение Все дети любят смотреть мультфильмы, предшествующее этому слову, – одна из посылок. Вторая же посылка Некоторые дети – школьники располагается после слов «так как», что и создает определенную трудность в выполнении этого упражнения. Получаем:
1. Все дети любят мультфильмы.
2. Некоторые дети – школьники.
 3. Некоторые школьники любят мультфильмы.
3. Некоторые школьники любят мультфильмы.
Дата добавления: 2016-09-20; просмотров: 1279;
