Равновесная ситуация
Пусть матричная игра m×n задана платежной матрицей
 =
= 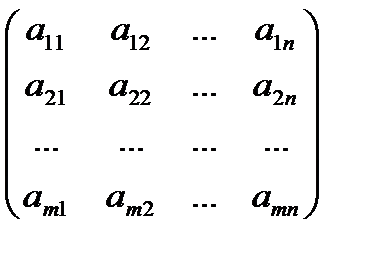 (4.2)
(4.2)
Строки этой матрицы соответствуют стратегиям игрока  , а столбцы – стратегиям игрока
, а столбцы – стратегиям игрока 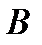 . В теории игр предполагается, что оба игрока действуют разумно, т.е. стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим для себя образом. Определим оптимальные стратегии каждого из игроков. Начнем с анализа стратегий игрока
. В теории игр предполагается, что оба игрока действуют разумно, т.е. стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим для себя образом. Определим оптимальные стратегии каждого из игроков. Начнем с анализа стратегий игрока  . На стратегию
. На стратегию 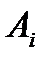 игрока
игрока  игрок
игрок 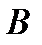 ответит такой стратегией
ответит такой стратегией 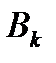 , при которой выигрыш игрока
, при которой выигрыш игрока  будет минимальным. Аналогично игрок B будет отвечать на все m стратегий игрока
будет минимальным. Аналогично игрок B будет отвечать на все m стратегий игрока  . Другими словами, найдем в каждой строке матрицы минимальный элемент (минимальные выигрыши игрока
. Другими словами, найдем в каждой строке матрицы минимальный элемент (минимальные выигрыши игрока  )
)

и запишем их в правом столбце табл. 4.2.
Таблица 4.2.
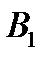
| 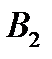
| … | 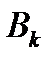
| … | 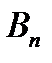
| Минимальные выигрыши игрока А | |
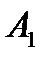
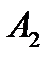 …
…
 …
…
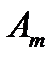
| 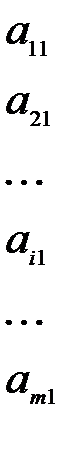
| 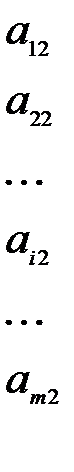
| 
| 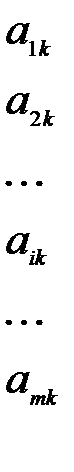
| 
| 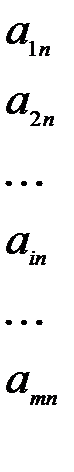
| 
|
| Максимальные выигрыши игрока А | 
| 
| 
| 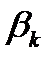
| 
| 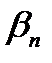
|
Действуя разумно, игрок  остановится на той стратегии
остановится на той стратегии  , для которой
, для которой 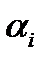 окажется максимальным. Поэтому среди чисел
окажется максимальным. Поэтому среди чисел 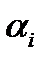
выбираем максимальное число
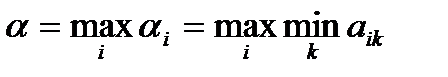 (4.3)
(4.3)
Число 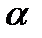 называется нижней ценой игры.
называется нижней ценой игры.
Принцип построения стратегии игрока  , основанный на максимизации минимальных выигрышей, называется принципом максимина (maxmin).
, основанный на максимизации минимальных выигрышей, называется принципом максимина (maxmin).
Проведем анализ стратегий игрока 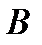 . Для этого найдем в каждом столбце матрицы максимальный элемент (максимальные выигрыши игрока
. Для этого найдем в каждом столбце матрицы максимальный элемент (максимальные выигрыши игрока  ):
):

и запишем их в нижней строке табл. 4.2. Действуя разумно, игрок B остановится на той стратегии 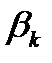 , для которой
, для которой 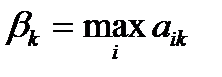 выбираем минимальное число
выбираем минимальное число

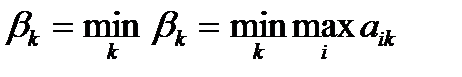 (4.4)
(4.4)
Число β называется верхней ценой игры.
Принцип построения стратегии игрока B, основанный на минимизации максимальных выигрышей, называется принципом минимакса (minmax).
Нижняя цена игра α и верхняя цена игра β связаны неравенством
α ≤ β. (4.5)
Если 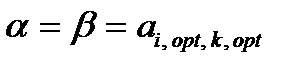 или
или
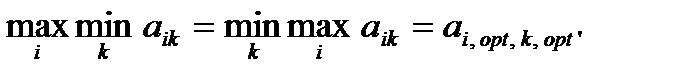 (4.6)
(4.6)
то ситуация 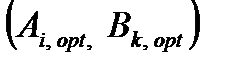 оказывается равновесной, и ни один игрок не заинтересован в том, чтобы ее нарушить. В том случае, когда верхняя цена игры равна нижней, их называют просто ценой игры.
оказывается равновесной, и ни один игрок не заинтересован в том, чтобы ее нарушить. В том случае, когда верхняя цена игры равна нижней, их называют просто ценой игры.
Если α=β, то такую игру называют также игрой с седловой точкой, а пара оптимальных стратегий 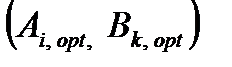 – седловой точкой матрицы. Цена игры обозначается буквой v. Тогда
– седловой точкой матрицы. Цена игры обозначается буквой v. Тогда  .
.
Седловых точек в матричной игре может быть несколько, но все они имеют одно и то же значение.
Пример 4.2. Игроки  и
и 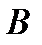 записывают одну из трех цифр: 1, 2 или 3. Затем сравнивают эти цифры и расплачиваются друг с другом так, как показано в платежной матрице размера 3×3 :
записывают одну из трех цифр: 1, 2 или 3. Затем сравнивают эти цифры и расплачиваются друг с другом так, как показано в платежной матрице размера 3×3 :
 =
= 
Определить оптимальные стратегии.
Решение. Здесь строки соответствуют стратегиям игрока  , а столбцы – стратегиям игрока
, а столбцы – стратегиям игрока 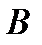 .
.
Стратегия игрока  :
: 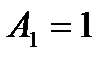 ;
; 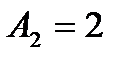 ;
;  .
.
Стратегия игрока 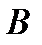 :
: 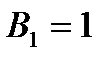 ;
; 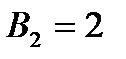 ;
; 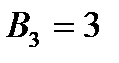 .
.
Определим оптимальные стратегии каждого из игроков. Начнем с анализа стратегий игрока  . Игрок
. Игрок  анализирует свою стратегию на максимин (maxmin) , т.е. на максимальный из своих минимальных выигрышей. На стратегию
анализирует свою стратегию на максимин (maxmin) , т.е. на максимальный из своих минимальных выигрышей. На стратегию  игрока
игрока  игрок В ответит стратегией
игрок В ответит стратегией  , т.е. то стратегией, при которой выигрыш игрока
, т.е. то стратегией, при которой выигрыш игрока  будет минимальным (выигрыш – 2 игрока
будет минимальным (выигрыш – 2 игрока  означает его выигрыш +2). На стратегию
означает его выигрыш +2). На стратегию  игрока
игрока  игрок В ответит стратегией
игрок В ответит стратегией 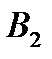 (минимальный выигрыш игрока
(минимальный выигрыш игрока  равен 1). На стратегию
равен 1). На стратегию 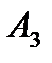 – стратегией
– стратегией 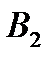 (минимальный выигрыш игрока
(минимальный выигрыш игрока  равен –3 ). Запишем минимальный выигрыш игрока А в правом столбце табл. 4.3.
равен –3 ). Запишем минимальный выигрыш игрока А в правом столбце табл. 4.3.
Таблица 4.3.
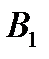
| 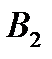
| 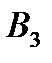
| Минимальные выигрыши игрока А | |
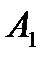

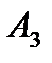
| -2 | -3 | -1 | -2 -3 |
| Максимальные выигрыши игрока А |
Игрок  , проанализировав правый столбец таблицы, оставит свой выбор на стратегии
, проанализировав правый столбец таблицы, оставит свой выбор на стратегии  , при которой его минимальный выигрыш максимален. Это максимальное значение называется максимин (maxmin). В данном случае maxmin = 1. Если игрок
, при которой его минимальный выигрыш максимален. Это максимальное значение называется максимин (maxmin). В данном случае maxmin = 1. Если игрок  будет придерживаться этой стратегии, то ему гарантирован выигрыш, не менее 1, при любом поведении противника.
будет придерживаться этой стратегии, то ему гарантирован выигрыш, не менее 1, при любом поведении противника.
Аналогично проведем анализ стратегий игрока 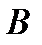 . Игрок В анализирует свою стратегию на минимакс (minmax), т.е. на минимальный из максимальных выигрышей игрока
. Игрок В анализирует свою стратегию на минимакс (minmax), т.е. на минимальный из максимальных выигрышей игрока  . На стратегию
. На стратегию 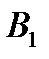 игрока
игрока 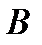 игрок
игрок  ответит стратегией
ответит стратегией 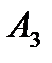 , т.е. той стратегией, при которой его выигрыш будет максимальным и равен 3. На стратегию
, т.е. той стратегией, при которой его выигрыш будет максимальным и равен 3. На стратегию  игрока
игрока 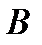 игрок
игрок  ответит стратегией
ответит стратегией 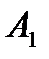 (его максимальный выигрыш равен 2), на стратегию
(его максимальный выигрыш равен 2), на стратегию 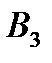 – стратегией
– стратегией 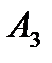 (его максимальный выигрыш равен 1). Запишем максимальные выигрыши игрока
(его максимальный выигрыш равен 1). Запишем максимальные выигрыши игрока  в нижней строке табл. 5.3. В данном случае minmax = 1. Если игрок В будет придерживаться этой стратегии, то он проиграет не больше 1 при любом поведении противника.
в нижней строке табл. 5.3. В данном случае minmax = 1. Если игрок В будет придерживаться этой стратегии, то он проиграет не больше 1 при любом поведении противника.
Таким образом, в рассматриваемой игре maxmin и minmax совпали:
maxmin =minmax = 1.
Таким образом, ситуация оказывается равновесной, матрица игры имеет седловую точку
 .
.
Дата добавления: 2016-09-20; просмотров: 1043;
