Матричные игры. Равновесная ситуация
Пусть в игре участвуют два игрока. Игрок 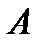 имеет m стратегий, а игрок
имеет m стратегий, а игрок 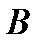 – n стратегий.
– n стратегий.
Обозначим стратегии игрока 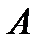 как
как 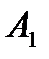 ,
, 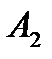 , …,
, …,  , а стратегии игрока
, а стратегии игрока 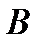 – как
– как  ,
, 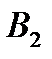 , …,
, …,  .
.
Если игрок  выбрал стратегию
выбрал стратегию 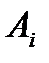 , а игрок
, а игрок 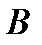 – стратегию
– стратегию 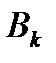 , то выигрыш игрока
, то выигрыш игрока  составит
составит 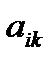 , а игрока
, а игрока 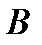 –
– 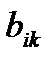 , причем
, причем
 = -
= - 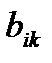 . (4.1)
. (4.1)
Поэтому при анализе такой игры достаточно рассмотреть выигрыш только одного игрока, например выигрыш  игрока А. Зная выигрыш аik по формуле (4.1) легко определить выигрыш
игрока А. Зная выигрыш аik по формуле (4.1) легко определить выигрыш 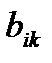 .
.
Матричные игры называются парными играми с нулевой суммой, в которых выигрыш одного игрока равен проигрышу другого.
Если известны все значения  для каждой пары стратегий {
для каждой пары стратегий { 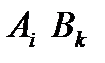 },
}, 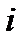 =1, 2, …, m,
=1, 2, …, m,  = 1, 2, …, n, то их удобно записать в виде прямоугольной таблицы, строки
= 1, 2, …, n, то их удобно записать в виде прямоугольной таблицы, строки  которой соответствуют стратегиям игрока
которой соответствуют стратегиям игрока  , а столбцы – стратегиям игрока В (табл. 4.1).
, а столбцы – стратегиям игрока В (табл. 4.1).
Таблица 4.1
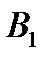
| 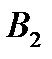
| … | 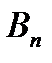
| |

 …
…

| 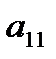
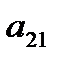 …
…

| 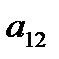
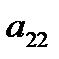 …
…
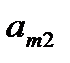
| … … … … | 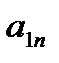
 …
…
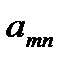
|
Чаще эти выигрыши записывают в виде платежной матрицы (матрицы игр) размера 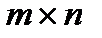 , поэтому такие игры называются матричными играми
, поэтому такие игры называются матричными играми 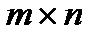 :
:
 А=
А= 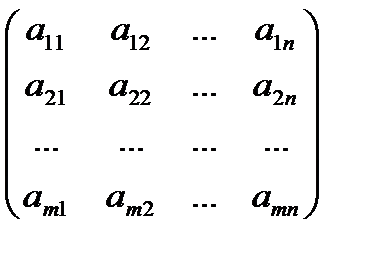
Матричные игры относятся к разряду антагонистических, т.е. игр, в которых интересы игроков противоположны.
Пример 4.1. Каждый из двух игроков  и
и 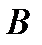 одновременно и независимо друг от друга записывают на листе бумаги любое целое число. Если записанные числа имеют одинаковую четность, то игрок
одновременно и независимо друг от друга записывают на листе бумаги любое целое число. Если записанные числа имеют одинаковую четность, то игрок  выигрывает одно очко, если разные, то одно очко выигрывает игрок
выигрывает одно очко, если разные, то одно очко выигрывает игрок 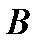 Построить платежную матрицу данной игры.
Построить платежную матрицу данной игры.
Решение. У игрока  две стратегии:
две стратегии: 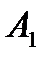 – записать четное число и
– записать четное число и 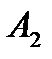 – записать нечетное число. У игрока
– записать нечетное число. У игрока 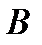 также две стратегии:
также две стратегии: 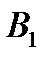 – записать четное число и
– записать четное число и 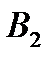 – записать нечетное число. Матрица выигрышей игрока
– записать нечетное число. Матрица выигрышей игрока  в этой игре 2×2 имеет вид
в этой игре 2×2 имеет вид
 =
= 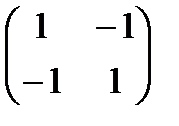 .
.
В данной матрице строки соответствуют стратегиям игрока 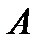 , а столбцы – стратегиям игрока
, а столбцы – стратегиям игрока 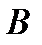 .
.
Действительно, если игрок  делает ход
делает ход 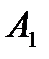 , а игрок
, а игрок 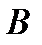 – ход
– ход  , то одно очко выигрывает игрок
, то одно очко выигрывает игрок  и
и 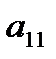 = 1. Если игрок
= 1. Если игрок  делает ход
делает ход 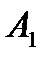 , а игрок
, а игрок 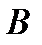 – ход
– ход 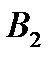 , то одно очко выигрывает игрок
, то одно очко выигрывает игрок 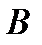 , соответственно игрок
, соответственно игрок 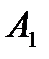 это очко проигрывает, т.е.
это очко проигрывает, т.е. 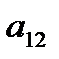 = -1 и т.д.
= -1 и т.д.
В примере 4.1 рассмотрена простейшая математическая модель конечной конфликтной ситуации, когда имеются два участника и выигрыш одного равен проигрышу другого. Такая модель называется антагонистической игрой двух лиц с нулевой суммой.
Дата добавления: 2016-09-20; просмотров: 1140;
