Основні поняття про комплексні числа. Дії з комплексними числами
Розрахунок кіл змінного струму з паралельно чи змішано з’єднаними споживачами за допомогою векторних діаграм володіє недоліком - дає похибку. Тому звичайно використовують аналітичний метод розрахунку змінних кіл - символічний метод. В основі цього методу лежать комплексні числа. Цими числами зображують синусоїдні величини (ЕРС, напруги, струми…), а також опори, провідності та потужності.
Символічний метод дозволяє замінити графічні дії з векторами на алгебраїчні дії з комплексними числами і використовувати для розрахунку кіл змінного струму усі методи розрахунку кіл постійного струму. Цей метод запропонував і запровадив у практику американський вчений Чарлз Протесу Штейнметц на початку 19 століття. Крім цього він займався електричними машинами і запропонував емпіричну формулу для визначення втрат у сталі.
Комплексними числами називають упорядковані пари дійсних та уявних чисел. Їх можна представити у трьох формах: алгебраїчній, показниковій та тригонометричній.
Алгебраїчна форма комплексного числа (скорочено комплекс числа) представляють як суму дійсного і уявного числа:
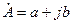 ,
,
де 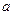 - дійсна частина комплексного числа, відкладається по вісі дійсних
- дійсна частина комплексного числа, відкладається по вісі дійсних
величин,
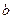 - коефіцієнт при уявній частині комплексного числа - по вісі уявних
- коефіцієнт при уявній частині комплексного числа - по вісі уявних
величин,
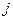 - це уявна одиниця.
- це уявна одиниця.
Уявне число дорівнює добутку уявної одиниці і коефіцієнта при ній. Для графічного зображення комплексу числа використовують прямокутну систему координат, де за горизонтальної віссю відкладають дійсні числа (цю вісь називають дійсною), а за вертикальною - уявні (цю вісь називають уявною), з урахуванням знаків (рис.18.1). З кінців отриманих відрізків проведемо перпендикуляри до їх перетину. З початку координат до точки перетину перпендикулярів проведемо вектор, який і зображує задане комплексне число.

Рисунок 18.1 - Графічне зображення комплексного числа
Таким чином, усякому комплексу на комплексній площині відповідає деякий вектор. З іншого боку проекція вектора на дійсну вісь дорівнює дійсній частини комплексу числа, а проекція вектора на уявну - коефіцієнту при уявній частині комплексу. Тоді, за малюнком можна записати тригонометричну форму комплексного числа:
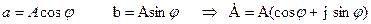 ,
,
де 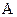 - модуль комплексного числа, визначається за теоремою Піфагора:
- модуль комплексного числа, визначається за теоремою Піфагора:
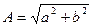
φ - кут між дійсною віссю та вектором комплексного числа (аргумент комплексного числа), визначається за тангенсом:
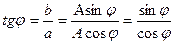
Позитивні аргументи комплексу відкладаються від дійсної позитивної вісі проти годинникової стрілки, негативні - за годинниковою стрілкою.
За формулою Ейлера 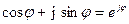 показникова форма комплексного числа буде:
показникова форма комплексного числа буде: 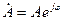 ,
,
де 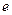 - основа натурального логарифму.
- основа натурального логарифму.
Операції множення та ділення у комплексних чисел зручно виконувати у показниковій формі. Добуток двох комплексів у показниковій формі є комплекс, модуль якого дорівнює добутку модулей окремих комплексів, а аргумент - алгебраїчній сумі їх аргументів:
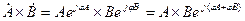
Результатом ділення двох комплексів у показниковій формі є комплекс, модуль якого дорівнює діленню модулей окремих комплексів, а аргумент - різниці їх аргументів:
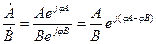
Таким чином, множення комплексного числа на 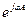 відповідає повороту вектора на
відповідає повороту вектора на 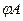 проти годинникової стрілки, якщо кут позитивний, і за годинниковою стрілкою, якщо кут негативний. Тому, уявну одиницю
проти годинникової стрілки, якщо кут позитивний, і за годинниковою стрілкою, якщо кут негативний. Тому, уявну одиницю 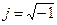 ще називають поворотним множником, так як множення на
ще називають поворотним множником, так як множення на 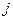 комплексу приводе до повороту вектора у позитивному напрямку на кут 90º. Помноження на
комплексу приводе до повороту вектора у позитивному напрямку на кут 90º. Помноження на 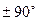 можна представити, як:
можна представити, як:
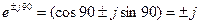
Спряженим комплексним числом називається число, яке має однаковий модуль з даним комплексом і відрізняється від нього лише знаком аргументу:
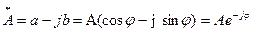
Множення комплексу на свій спряжений комплекс дорівнює:
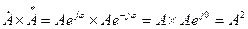
Операції складення та віднімання у комплексних чисел зручно виконувати у алгебраїчній формі. При цьому складають або вираховують окремо дійсні та уявні частини комплексу:
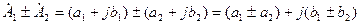
Так як комплекс можна представити вектором, то складання і віднімання відповідає цим операціям з векторами.
Зведення у ступень:
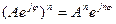
Вилучити корінь:
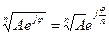
Дата добавления: 2016-09-20; просмотров: 1581;
