Кругові та топографічні діаграми

При зміні параметра кола (активного опору, ємності чи індуктивності) для струмів і напруг на окремих ділянках кола будуть різні значення. Проаналізувати зміну режимів кола можна побудовою серії векторних діаграм. Кругові діаграми - це серії векторних діаграм при зміні параметрів кола. Їх використовують для визначення струму чи напруги при певному значенні параметру, який змінюється (активного опору, ємності чи індуктивності). Наприклад, визначати значення струму при активному опорі, який дорівнює 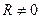, для вказаного на рис.20.1 кола. Активний опір можна змінювати. До цього кола подається синусоїдна напруга: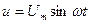

Рисунок 20.1 - Нерозгалужене коло зі змінним активним опором і його кругові діаграми

Рисунок 20.2 - Топографічна діаграма кола вказаного на рис.20.1

Побудуємо кругові діаграми (рис.20.1).

Відкладаємо вектор комплексу напруги: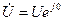

При R=0 спостерігається коротке замкнення. При цьому режимі струм у колі найбільш можливий: 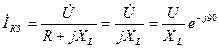, і відстає від напруги на кут 90º. Показуємо це на діаграмі і проводимо окружність з діаметром 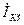. Уздовж вектора 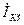відкладаємо відрізок ОК, який у масштабі дорівнює 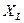. З точки К проведемо перпендикуляр цьому вектору - відрізок КП, який у масштабі дорівнює 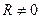, при якому струм у колі зменшується: 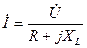. Якщо з’єднати прямою лінією точки О і П отримаємо точки 1 і 2 на кругових діаграмах, які і визначать режим роботи при заданому активному опорі 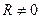: діюче значення струму - відрізок О1, який нахилений під кутом φ до вектора напруги, активна складова прикладеної до кола напруги - відрізок О2, реактивна складова прикладеної до кола напруги - відрізок ОА.

Напруга між двома точками електричного кола уявляє собою різницю потенціалів цих точок. Тобто, потенціал окремої точки можна представити відповідним комплексом потенціалу і зобразити вектором, який починається у початку координат. Його кінець позначають той же цифрою або буквою, що і точку кола, потенціал якої зображає вектор.

Топографічною діаграмою називається векторна діаграма комплексів кола при умові, що кожній точці кола відповідає певна точка на діаграмі і вектор, проведений з початку координат в будь-яку точку діаграми, зображає комплекс потенціалу цієї точки. В цьому випадку відрізок, який з’єднує дві будь-які точки діаграми, визначає комплекс напруги між цими точками.

При побудові топографічної діаграми потенціал будь-якої точки приймають рівним нулю і на діаграмі точку нульового потенціалу суміщають з початком координат.

Приклад, побудувати топографічну діаграму для вказаного на рис.20.1 кола.

Розв’язання

1 Визначимо точки в колі, де можлива зміна потенціалу. Позначимо їх 1, 2, 3. Потенціал точки 1 приймемо рівним нулю: 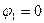. Початкову фазу загального струму приймемо рівною нулю, тобто: 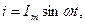тому вектор струму направлений уздовж позитивної дійсної вісі. Визначимо напрямки струмів та потенціалів у колі.

2 Складаємо рівняння потенціалів для кожної точки: 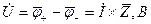. Струм в опорах добутково направлений від точки з більш високим потенціалом до точки з меншим потенціалом. Обхід контуру приймемо назустріч струму.

2: 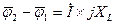, тоді

Вектор 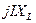випереджає струм за фазою на кут 90º - отримаємо точку 2.

3: 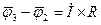, тоді

Вектор 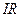збігається за напрямком з вектором струму - точка 3.

Вектор, який з’єднує точки 1 і 3, направлений від точки 3 до точки 1 зображує напругу на зажимах кола: 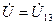. При цьому вектори напруг на діаграмі мають до точок кола напрямки зворотні позитивним напрямкам напруг відносно цих точок, що відповідає правилу віднімання векторів, згідно якому вектор різниці завжди направлений в один бік з вектором, від якого вираховують. Так вектор індуктивної напруги на топографічній діаграмі направлений від точки 1 до точки 2, у схемі направлений навпаки - від точки 2 до точки 1 (за напрямком струму).

Топографічна діаграма вказана на рис.20.2.

20.2 Одержання кута зсуву фаз 90°

Іноді в електричних колах потрібно отримати певний кут зсуву фаз між прикладеною до кола напругою та струмом в одній з гілок для зручності вимірювання деякої величини. Наприклад для кола з послідовно з’єднаними котушками з 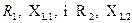потрібно отримати кут зсуву фаз 90º між прикладеною напругою та струмом . Так як у колі присутній активний опір, то зсув фаз менший за 90º. Для цього потрібно зашунтувати одну з котушок (ввімкнути паралельно до котушки) резистором з величиною опору:

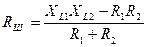
Аналогічно інші види навантаження. При паралельному сполученні зашунтовують ту гілку, в якій протікає потрібний струм.

Приклад розрахунку

Розглянемо розрахунок кіл змінного струму за допомогою комплексних чисел на прикладі методу згортання.

До вказаного на рис.20.3 кола подається змінна напруга 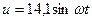. Визначити усі струми і спад напруги на першому елементі при: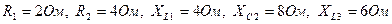

Рисунок 20.3 - Задане розгалужене коло змінного струму

Розв’язання

1 Проставимо напрямок струмів та нумерацію вузлів.

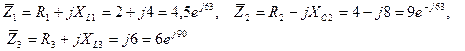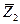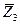2 Повні опори кола у комплексній формі будуть: Так як та з’єднанні паралельно, то

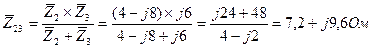
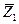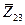3 Так як та з’єднанні послідовно, то

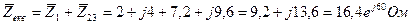
4 Комплекс прикладеної до кола напруги: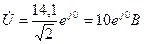

5 Згідно закону Ома:

.

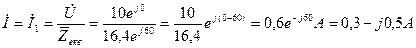6 Падіння напруги на першому опорі:

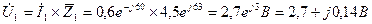
7 При паралельному сполученні

8 Тоді згідно закону Ома:

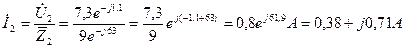
9 Згідно І закону Кірхгофа:

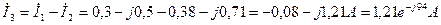
10 Виконаємо перевірку вірного вирішення за допомогою балансу потужностей. Потужність, яка споживається усім колом: ,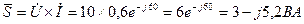

тобто активна потужність кола: ,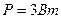

а реактивна 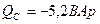і характер навантаження ємнісний.

11 Потужності окремих споживачів:

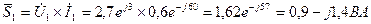
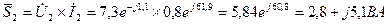
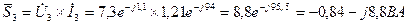
Баланс потужностей: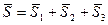

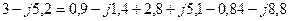
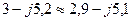. Перевірка збігається.

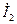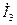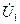12 Виконаємо перевірку за допомогою векторних діаграм (рис.20.4). Векторні діаграми будуються у масштабі. На діаграмі струмів при складанні векторів та повинні отримати вектор . На діаграмі напруг при складанні векторів та 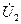повинні отримати вектор .

13 Миттєві значення струмів: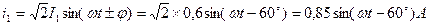

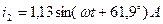
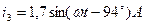
Рисунок 20.4 - Векторні діаграми струмів і напруг для кола вказаного на рис.20.3