Додавання та віднімання синусоїдних величин

На одній векторній діаграмі векторами зображують величини лише однієї певної частоти, таким чином, обертання векторів відбувається з однією кутовою частотою, тобто їх взаємне розміщення залишається незмінним. При зрівнянні синусоїдних величин початок відрахування можна обрати довільно, тобто один із векторів можна направити довільно, а інші вектори потрібно розміщати по відношенню до першого під кутами, які дорівнюють відповідним кутам зсуву фаз. При цьому позитивні кути відкладають проти годинникової стрілки від першого вектора, а негативні - за годинниковою стрілкою. Розміщення векторів відносно один одного не залежить від того, який момент часу прийнятий за початковий.

При розрахунках кіл змінного струму потрібно виконувати складання чи вирахування синусоїдних величин, які мають однакову частоту, але різні амплітуди та початкові фази.

За допомогою векторних діаграм можна виконувати арифметичні операції зі змінними величинами для розрахунку електричних кіл.

Наприклад, для електричного вузла визначити струм 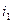, якщо відомі струми:

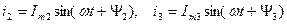
Частота мережі 50Гц (тобто кутова частота для усіх струмів однакова).

1 Визначимо миттєве значення струму за І законом Кірхгофа:

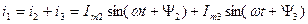
Операцію складання виконаємо за допомогою діаграм.

2 Визначимо струм 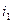за допомогою хвильової діаграми (рис.4.1). Для цього побудуємо синусоїди відомих струмів і для отримання сумарної кривої потрібно для кожного моменту часу скласти ординати відомих синусоїд.

3 Визначимо струм 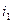за допомогою векторної діаграми (рис.4.2). Для цього відкладаємо відомі струми у масштабі й за правилом складання векторів (правило паралелограма) знаходимо вектор струму:

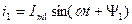
Рисунок 4.1 - Складання струмів за допомогою хвильових діаграм

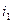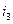Якщо за відомими струмами та треба визначити 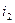, то для віднімання векторів можна використати правило трикутника. Віднімання двох векторів замінюють складання цих двох величин, лише ту величину, яку вираховують беруть негативною:

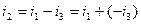
Потрібно пам’ятати, що зміна знака у синусоїди відповідає зміні початкового фазного кута на 180º:

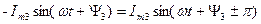
У векторів це означає поворот вектора на ±180º.

Рисунок 4.2 - Складання струмів за допомогою векторних діаграм

Таким чином, при складанні чи відніманні гармонічних величин однієї частоти отримуємо гармонічну величину той же частоти, амплітуда якої дорівнює геометричній сумі чи різниці амплітуд відомих величин:

,

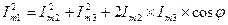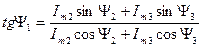
де 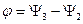- зсув фаз між 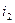та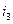

Перевагою зображення синусоїдних величин векторами є у тому, що при такому зображенні сума та різниця кількох величин може бути визначена графічно швидко і просто, у той час як при зображенні величин синусоїдами ці операції складні і потребують багато часу.

У випадку складання двох гармонічних величин зі зсувом фаз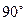

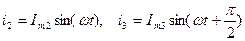
отримаємо: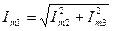

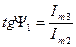
У випадку складання двох гармонічних величин з однаковими початковими фазами 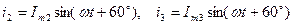отримаємо:

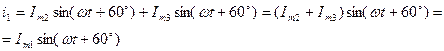
При складанні двох синусоїдних величин різної частоти отримуємо несинусоїдну величину, яка не може зображатися вектором, який обертається.

При більшій кількості векторів їх складання виконується методом багатокутника, тобто вектори переносяться паралельно самим себе так, щоб початок другого вектора збігався з кінцем першого і так далі. Замикаючий вектор зображує сумарну величину.

Приведені положення про геометричне складання векторів синусоїдних струмів однакової частоти відносяться і до інших синусоїдних величин.