Обратная геодезическая задача
Обратная геодезическая задача состоит в том, что по известным координатам конечных точек линии 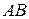 вычисляют дирекционный угол и горизонтальное проложение этой линии, т.е. известны
вычисляют дирекционный угол и горизонтальное проложение этой линии, т.е. известны 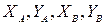 , необходимо определить
, необходимо определить 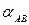 и
и 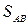 .
.
Задача решается двумя способами, но предварительно необходимо вычислить приращения координат, следуя правилу: приращение координат равно разности координат конечной и начальной точек линии. Эти вычисления бесконтрольные, поэтому приращения необходимо вычислять с особым вниманием.
Первый способ:
Вначале вычисляют дирекционный угол по формуле
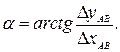
Для однозначного определения дирекционного угла следует учитывать знаки приращений координат. Соотношения между величиной дирекционного угла, названием румба и знаками приращений приведены в таблице 1.1.
Таблица 1.1.
| Дирекционный угол линии | Название румба | Знаки приращений координат | |
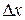
| 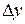
| ||
0 - 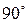
| СВ | + | + |
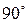 - - 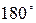
| ЮВ | - | + |
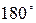 - - 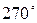
| ЮЗ | - | - |
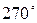 - - 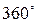
| СЗ | + | - |
Горизонтальное проложение вычисляют по формулам:
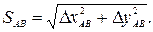
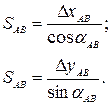
Сходимость результатов вычисления 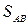 контролирует вычисление дирекционного угла и горизонтального проложения, но не контролирует вычисление приращений.
контролирует вычисление дирекционного угла и горизонтального проложения, но не контролирует вычисление приращений.
Второй способ.
По вычисленным приращениям координат вычисляют горизонтальное проложение
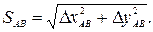
Далее дважды вычисляют дирекционный угол
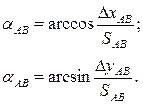
Дата добавления: 2016-09-20; просмотров: 2077;
