Расчет случайной погрешности химических анализов
| Порядковый номер пробы n | Содержание меди, % | x y | (x y)2 | ||
| Основные пробы x | Контрольные пробы y | ||||
| 2,79 | 2,98 | -0,19 | 0,0361 | ||
| 1,30 | 1,12 | 0,18 | 0,0324 | ||
| 1,37 | 1,51 | -0,14 | 0,0196 | ||
| 2,97 | 2,90 | 0,07 | 0,0049 | ||
| 0,51 | 0,54 | -0,03 | 0,0009 | ||
| 1,20 | 1,12 | 0,08 | 0,0064 | ||
| 2,28 | 2,33 | -0,05 | 0,0025 | ||
| 1,01 | 0,97 | 0,04 | 0,0016 | ||
| 1,08 | 1,29 | -0,21 | 0,0441 | ||
| 2,24 | 2,09 | 0,15 | 0,0225 | ||
| 1,41 | 1,55 | -0,14 | 0,0196 | ||
| 0,64 | 0,64 | 0,00 | 0,0000 | ||
| 1,20 | 1,15 | 0,05 | 0,0025 | ||
| 1,56 | 1,74 | -0,18 | 0,0324 | ||
| 2,92 | 2,78 | 0,14 | 0,0196 | ||
| 2,64 | 2,69 | -0,05 | 0,0025 | ||
| 1,36 | 1,28 | 0,08 | 0,0064 | ||
| 2,97 | 3,18 | -0,21 | 0,0441 | ||
| 3,17 | 3,08 | 0,09 | 0,0081 | ||
| 2,40 | 2,54 | -0,14 | 0,0196 | ||
| 1,66 | 1,55 | 0,11 | 0,0121 | ||
| 1,53 | 1,39 | 0,14 | 0,0196 | ||
| 2,32 | 2,56 | -0,24 | 0,0576 | ||
| 3,30 | 3,17 | 0,13 | 0,0169 | ||
| 0,64 | 0,78 | -0,14 | 0,0196 | ||
| ___________________________ Сумма 46,47 | 46,93 | - | 0,4516 | ||
| Среднее | 1,86 | 1,88 | - | - |
Имеем среднее содержание по основным пробам xср = 1,86 %, среднее по контрольным пробам yср = 1,88 %, среднеквадратичная случайная погрешность анализов
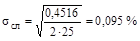 .
.
Относительная случайная погрешность
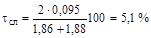 .
.
Относительная погрешность находится в допустимых пределах (см. табл.15), следовательно, результаты химических анализов удовлетворительные.
Гибкий подход рекомендован в методических указаниях [18]. Согласно им выделяются классы точности анализов в зависимости от отношений z вычисленной случайной погрешности к допустимой:
| Класс точности анализов | Значение коэффициента z | Примечание |
| I | < 0,33 | Количественные анализы |
| II | 0,33-0,5 | " |
| III | 0,5-1 | " |
| IV | 1-2 | " |
| V | < 2 | Полуколичественные анализы |
Отсюда следует, что для подсчета запасов главных компонентов пригодны только анализы I-III классов точности.
Изучение систематических погрешностей
Систематические погрешности изучают как при опробовании в целом, так и при выполнении отдельных операций.

Систематические погрешности выявляются путем сопоставления совмещенных основных и контрольных проб, исследованных в неравноточных условиях: контрольные пробы исследуются с повышенной точностью по сравнению с основными.
Так, при изучении систематических погрешностей взятия проб контрольные пробы берут более надежным способом. Отбор проб из скважин контролируется отбором проб из горных выработок, совмещенных со скважинами. Бороздовые пробы малого сечения контролируются бороздовыми пробами большого сечения или валовыми пробами и т.д. Для выявления систематических погрешностей анализов дубликаты основных проб направляют на исследование в другую лабораторию, эта операция называется внешним контролем анализов. В случае существенных расхождений между результатами основных и контрольных проб те же дубликаты могут быть направлены в специализированную лабораторию на арбитражный контроль анализов. Для контроля необходимо иметь несколько десятков контрольных проб за определенный отрезок времени (например, за год), как и при выявлении случайных погрешностей.
Изучение систематических погрешностей начинается с исследования зависимости между основными и контрольными пробами графическим (рис.14) и аналитическим путем. На основе статистических характеристик вычисляется критерий t:
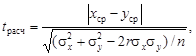 (3)
(3)

|
где xср и yср средние значения соответственно по основным и контрольным пробам; 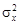 и
и 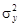 соответствующие дисперсии содержаний; r коэффициент корреляции между основными и контрольными содержаниями; n число контрольных проб.
соответствующие дисперсии содержаний; r коэффициент корреляции между основными и контрольными содержаниями; n число контрольных проб.
Если критерий tрасч равен или больше допустимого t, то систематическое расхождение между основными и контрольными пробами доказано.
Согласно методическим указаниям [19] допустимое значение критерия t находится по таблицам распределения Стьюдента при вероятности появления ошибок 0,05 (табл.17). На значение критерия влияет количество имеющихся степеней свободы k, которое зависит от числа контрольных проб: k = n 1. При увеличении числа контрольных проб распределение Стьюдента приближается к нормальному и в пределе, при k = ¥, совпадает с ним. Практически при числе проб 30 и более можно принимать tрасч = 2.
Как следует из формулы (3), наличие систематических расхождений выявляется сравнением средних содержаний xср и yср, что не всегда эффективно.
Возможна ситуация "перекрестной" систематической ошибки, когда средние совпадают, но имеются существенные расхождения при высоких и низких содержаниях разного знака, в среднем компенсирующие друг друга. В этом случае предлагается вычислять уравнение линейной регрессии y = ax + b, которое выражается через статистические характеристики:
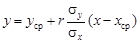 .
.
Таблица 17
Дата добавления: 2016-05-05; просмотров: 1861;
