Одноразрядные полные сумматоры
Лекция 17. Комбинаторные логические схемы.
Генераторы. Часть 1.
Комбинационные схемы
Устройство, преобразующее дискретную информацию, в общем случае имеет n входов для входных сигналов и m выходов, с которых снимаются выходные сигналы.
Преобразование информации в МПС производится электронными устройствами (логическими схемами) 2-х типов (рис. 1): комбинационными схемами (КС) и цифровыми автоматами (ЦА).

|
Рис. 1. Электронные устройства преобразования информации.
В комбинационных схемах совокупность выходных сигналов (выходное слово Y) в любой момент времени однозначно определяется входными сигналами (входным словом Х), поступающими на входы в тот же момент времени. Реализуемый в комбинационных схемах способ обработки информации зависит только от комбинации входных сигналов и выходные сигналы вырабатываются сразу же после подачи входной информации.
Закон функционирования КС задается либо с помощью таблицы соответствия входных и выходных слов, либо в аналитической форме с использованием логических функций.
Комбинационная схема является техническим аналогом булевой функции и выполняет соответствующее этой функции преобразование информации. Число входов КС должно равняться числу аргументов булевой функции, а число ее выходов - количеству компонентов вектора Y={y1, y2, ..., yk}, если логическая функция является векторной.
Полусумматоры
Полусумматором называется комбинационная схема с двумя входами и двумя выходами, на которых вырабатываются сигнал суммы и переноса согласно правилам двоичной арифметики (рис. 2).
Правила двоичной арифметики при сложении двух одноразрядных двоичных чисел ai и bi имеют вид:
| ai | bi | pi | si |
где si - сумма двух однобитовых чисел, pi - перенос в старший разряд.
Из таблицы соответствия видно, что выходные сигналы комбинационной схемы полусумматора описываются функциями:
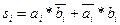 pi = ai * bi
pi = ai * bi
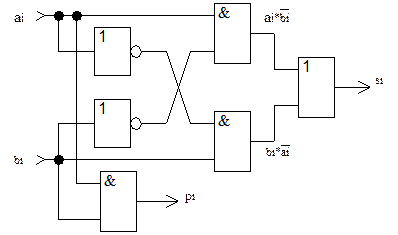
Отсюда принципиальную схему полусумматора на базе простейших логических элементов можно, например, реализовать в следующем виде:
|

|
Рис. 2. Принципиальная схема и условное обозначение полусумматора:
Одноразрядные полные сумматоры
Одноразрядный полный сумматор имеет 3 входа и 2 выхода и обеспечивает сложение двух одноразрядных слагаемых с учетом переноса из младшего разряда (рис. 3).
| ai | bi | pi-1 | si | pi |

|
Рис. 3. Условное обозначение и таблица соответствия одноразрядного сумматора.
Из таблицы соответствия получаем, что комбинационная схема полного сумматора должна реализовывать следующие логические функции:
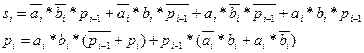
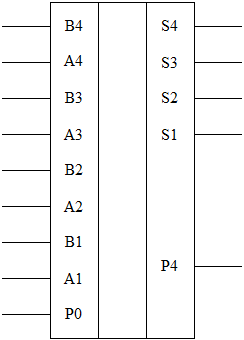
На основе одноразрядных полных сумматоров и полусумматоров можно реализовать многоразрядных сумматоры, приведенный на рис. 4.
|
Рис. 4. Четырехразрядный сумматор К155ИМ3
Чтобы получить из сумматора К155ИМ3 сумматор, приведенный на левом рисунке, необходимо вход Р0 подключить к земле.
С помощью сумматоров можно производить как сложение многоразрядных двоичных чисел, так и их сдвиги влево. Например, сдвиг двоичного числа на один разряд влево осуществляется простым сложением этого числа с самим собой (умножение на 2): 1011+1011=10110. Это позволяет реализовать операции умножения и деления двоичных чисел, т.к. известно, что мультипликативные операции сводятся к операциям сложения (вычитания) и сдвигам.
Таким образом, n-разрядный сумматор представляет собой один из центральных элементов арифметико-логического устройства (АЛУ) микропроцессора, с помощью которого выполняются арифметические операции над числами с плавающей и фиксированной точкой.
Дешифраторы
Линейный или одноступенчатый дешифратор. Дешифратор - это комбинационное устройство, предназначенное для преобразования параллельного двоичного кода в унитарный, т.е. позиционный код. Обычно, указанный в схеме номер вывода дешифратора соответствует десятичному эквиваленту двоичного кода, подаваемого на вход дешифратора в качестве входных переменных, вернее сказать, что при подаче на вход устройства параллельного двоичного кода на выходе дешифратора появится сигнал на том выходе, номер которого соответствует десятичному эквиваленту двоичного кода. Отсюда следует то, что в любой момент времени выходной сигнал будет иметь место только на одном выходе дешифратора. В зависимости от типа дешифратора, этот сигнал может иметь как уровень логической единицы (при этом на всех остальных выходах уровень логического 0), так и уровень логического 0 (при этом на всех остальных выходах уровень логической 1). Пирамидальные дешифраторы позволяют реализовать схему на базе только двухвходовых элементов логического умножения (конъюнкции). Рассмотрим пример реализации дешифратора 3®8 (три входа и восемь выходов), который приведен на рис. 5.
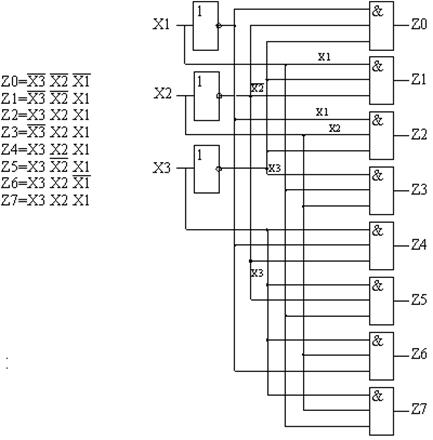
Рис. 5. Схема дешифратора 3 на 8.
Для построения такого дешифратора потребуется 12 двухвходовых элементов 2И и три инвертора. Пирамидальные дешифраторы при больших количествах входных переменных позволяют несколько упростить конструкцию устройства, т.е. уменьшить количество интегральных микросхем.
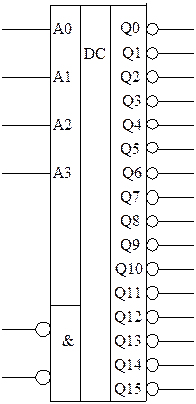
|
Промышленностью выпускаются различные модификации дешифраторов в интегральном исполнении. Обозначение дешифраторов на принципиальных схемах показано на рис. 6.
Рис. 6. Обозначение дешифратора К1533ИД3.
В дешифраторах часто предусматривается операция стробирования, посредством которой выработка выходных сигналов разрешается только в момент подачи управляющего строба. Так, для ИМС К1533ИД3 выходы активизируются при одновременной подаче логического нуля на управляющие входы &.
Рассмотрим пример каскадного дешифратора для пятиразрядного двоичного кода. Каждый дешифратор выполнен с управляющими входами, объединенными конъюнктивно. При выполнении условия конъюнкции на выходе, номер которого соответствует десятичному эквиваленту двоичного кода, появится уровень логического “0”. В противном случае все выходы находятся в состоянии логической единицы (рис.2.3). Как следует из рис. 7, пятиразрядный дешифратор, имеющий 32 выхода, выполнен на базе четырех дешифраторов с использованием лишь одного дополнительного инвертора, что достигнуто благодаря наличию входной управляющей логики каждой интегральной микросхемы. Нетрудно заметить, что входная логика дешифраторов КР1533ИД7 позволяет реализовать функцию дешифратора 2®3 без дополнительных элементов, а полного дешифратора 2®4 с использованием одного инвертора.
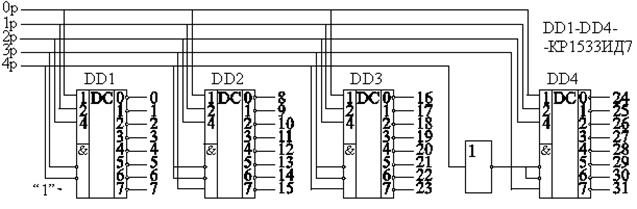
Рис. 7. Схема полного пятиразрядного дешифратора на 32 выхода.
Шифраторы
Двоичные шифраторы преобразуют унарный код (один из Nn) в двоичный код, т.е. выполняют операцию, обратную операции дешифраторов. При возбуждении одного из входов шифратора на его выходах формируется слово, отображающее номер возбуждаемой линии в двоичной системе счисления. Полный двоичный шифратор имеет 2n входов и n выходов.
Одно из основных применений шифратора - это ввод данных с клавиатуры, при котором нажатие произвольной цифровой клавиши должно приводить к передаче в устройство соответствующего данной цифре двоичного кода.
Мультиплексоры
Мультиплексоры традиционно используются для поочередной передачи данных от нескольких входных каналов в один выходной канал. Каждый из входных каналов подключается к выходному каналу под управлением адресующего сигнала.
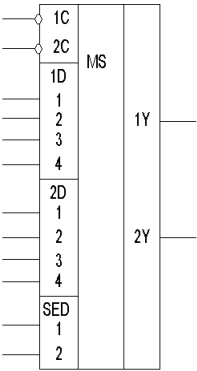
Приведенный на рис. 8. мультиплексор КР1533КП2 представляет собой сдвоенный селектор-мультиплексор 1 из 4-х с общими входами выбора данных SED и раздельными входами стробирования 1C, 2C.
Входы мультиплексора делятся на 2 группы - информационные (1D, 2D) и управляющие (1C, 2C, SED). Двоичный управляющий код SED задает положение переключателя, соединяющего один из входов с выходом мультиплексора в соответствии со следующей таблицей соответствия:
|
| SED1 | SED2 | i |
Рис. 8. Схема мультиплексора КР1533КП2.
Управляющие входы 1С, 2С используются для выбора кристаллов:
1С=1 - выход 1Y находится в высокоимпедансном состоянии;
1С=0 - выход 1Y подключен к одному из входов 1Di (номер входа задается сигналами SED);
2С=1 - выход 2Y в высокоимпедансном состоянии;
2С=0 - выход 2Y подключен к одному из входов 2Di.
В данном примере рассмотрен двухшинный мультиплексор на 4 направления, однако в сериях интегральных микросхем (ИМС) имеются и другие мультиплексоры: одношинный на 16 направлений, одношинный на 8 направлений, четырехшинный на 2 направления и др.
Мультиплексоры на большее число входов строятся путем объединения нескольких мультиплексоров меньшей размерности.
| <== предыдущая лекция | | | следующая лекция ==> |
| Комплиментарная МДП логика | | | Формирователи импульсов. Лекция 18. Комбинаторные логические схемы. |
Дата добавления: 2016-09-20; просмотров: 3627;
