Свойства равномерно сходящихся рядов
Теорема.(Непрерывность суммы ряда) Если члены ряда 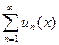 - непрерывные на отрезке
- непрерывные на отрезке  функции и ряд сходится равномерно, то и его сумма
функции и ряд сходится равномерно, то и его сумма 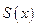 является непрерывной функцией на отрезке
является непрерывной функцией на отрезке  .
.
Теорема. (О почленном интегрировании ряда) Равномерно сходящийся на отрезке  ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку
ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку  , сходится к интегралу от суммы ряда по этому отрезку.
, сходится к интегралу от суммы ряда по этому отрезку.
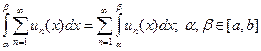
Теорема.(О почленном дифференцировании ряда) Если члены ряда 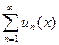 сходящегося на отрезке
сходящегося на отрезке  представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных
представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных 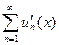 сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
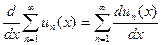
На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
На практике часто применяется разложение функций в степенной ряд.
Степенные ряды
Определение. Степенным рядомназывается ряд вида;
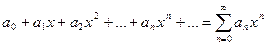 .
.
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Пример. Исследовать на сходимость ряд 
Применяем признак Даламбера:
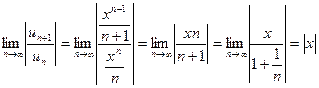 .
.
Получаем, что этот ряд сходится при 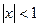 и расходится при
и расходится при 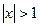 .
.
Определим сходимость в граничных точках 1 и –1.
При 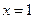 имеем:
имеем: 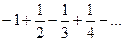 ряд сходится по признаку Лейбница
ряд сходится по признаку Лейбница
При 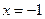 имеем:
имеем: 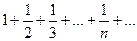 ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд).
Теоремы Абеля
Теорема.(Первая теорема Абеля) Если степенной ряд 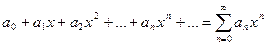 сходится при
сходится при 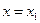 , то он сходится и притом абсолютно для всех
, то он сходится и притом абсолютно для всех 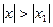 .
.
Доказательство. По условию теоремы, так как члены ряда ограничены, то
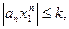
где k- некоторое постоянное число. Справедливо следующее неравенство:

Из этого неравенства следует, что при 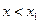 численные величины членов нашего ряда будут меньше (во всяком случае не больше ) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии
численные величины членов нашего ряда будут меньше (во всяком случае не больше ) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии 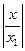 по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.
по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.
На основании признака сравнения делаем вывод, что ряд 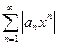 сходится, а значит ряд
сходится, а значит ряд 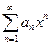 сходится абсолютно.
сходится абсолютно.
Таким образом, если степенной ряд 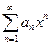 сходится в точке
сходится в точке 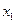 , то он абсолютно сходится в любой точке интервала длины
, то он абсолютно сходится в любой точке интервала длины 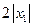 с центром в точке
с центром в точке  .
.
Следствие. Если при 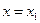 ряд расходится, то он расходится для всех
ряд расходится, то он расходится для всех 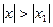 .
.
Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что 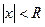 ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех 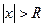 ряд расходится. При этом число R называется радиусом сходимости. Интервал
ряд расходится. При этом число R называется радиусом сходимости. Интервал 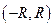 называется интервалом сходимости.
называется интервалом сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым. Радиус сходимости может быть найден по формуле:
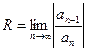 .
.
Пример. Найти область сходимости ряда 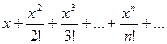
Находим радиус сходимости 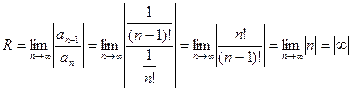 .
.
Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю:
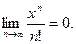
Теорема. (Вторая теорема Абеля) Если степенной ряд 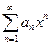 сходится для положительного значения
сходится для положительного значения 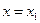 , то он сходится равномерно в любом промежутке внутри
, то он сходится равномерно в любом промежутке внутри 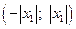 .
.
Дата добавления: 2016-05-05; просмотров: 722;
