Гистограмма распределения

Интер- валы
mi
pi = =

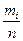
Очевидно, что площадь элементарного прямоугольника

s_i = hy_i, = p_i, (9.10)

а площадь всей гистограммы

S = 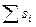= = 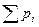1. (9.11)

Таким образом, гистограмма представляет собой совокупность прямоугольников (рис. 9.1).

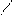
f(X) 2

1

Х

Рис. 9.1. Гистограмма (1) и полигон (2) распределения

величины Х

F(X)

1

Х

Рис. 9.2. Статистический ряд распределения

Полигон (рис. 9.1, кривая 2) строят как ломаную пря-мую, соединяющую середины интервалов.

В пределе гистограмма (полигон) стремится к нормальному закону распределения, плотность функции распределения которого описывается уравнением (9.12).

В качестве закона распределения случайных величин чаще всего используют нормальный закон распределения, или закон Гаусса (K.F. Gauss – немецкий математик ХIХ века).

Плотность нормального закона распределения описывают уравнением

f(x) = 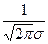e 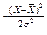. (9.12)

Функция плотности распределения позволяет определить вероятность появления данного конкретного значения Х.

Данные, снятые для построения гистограммы и полигона, могут быть использованы для построения статистического ряда распределения (рис. 9.2).

Статистический же ряд распределения стремится к функции распределения, которая описывается следую-щим уравнением:

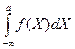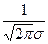
F(X) = = 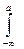e 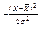dX. (9.13)

Функция распределения позволяет определить вероятность появления значения Х в интервале от - 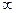до числа а.

Критерий (греч. kriterion - мерило) 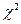Пирсона (К. Pearson – английский математик, биолог и философ ХIХ – ХХ веков) – один из важнейших непараметрических критериев. С его помощью проверяют гипотезу (греч. hipotesis – основание, предположение) о согласии выборочного распределения с нормальным законом распределения. Применение распределения 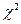допусти-мо лишь тогда, когда np_i ³ 5.

Для проведения проверки нормальности закона распределения заполняют таблицу (см. табл. 9.2).

Таблица 9.2

Проверка по критерию 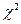Пирсона

Начало интер- вала	mi	ti	Ф(ti)	p¢i	mi-np¢i	(mi-np¢i)2 np¢i
… … …
Сумма		---	---		---

Первые два столбца заполняют данными из табл. 9.1. В третьем столбце записывают отношение

t_i = 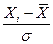. (9.14)

Четвёртый столбец заполняют соответствующими значениями интеграла вероятностей Ф(t_i) из справочной литературы или приложения данного практикума.

Интеграл (лат. integer – целый) вероятностей равен

Ф(t) = 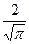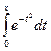, (9.15)

где t = .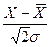

По значениям Ф(_i) в пятом столбце вычисляют вероятность p¢_i какразность соответствующих значений Ф(t)

p¢_i = Ф(t_i) - Ф(t_i-1). (9.16)

Напомним, что Ф( 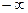) = - 0,5.

Последние столбцы таблицы в пояснении не нуж-даются.

Сумма чисел последнего столбца даёт значение

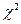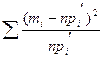= , (9.17)

где n – число всех результатов измерений.

Если 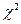окажется больше критического значения 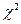_крит при некоторой доверительной вероятности Р и числе степеней свободы k = l - 3, где l – число всех интервалов, то с надёжностью Р можно считать, что распределение вероятностей результатов измерения в рассматриваемой серии измерений отличается от нормального. В противном случае для такого вывода нет достаточных оснований.

Указанное число степеней свободы k = l – 3 относится только к тому случаю, когда оба параметра нормального закона распределения определяют по результатам измерений, т.е. когда вместо точных значений Х и 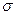применяют их эмпирические оценки. Если значение Х известно точно (например, при измерении эталона), то число степеней свободы равно k = l – 2.

Для измерительного канала погрешность измерения d равна

d = 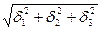, (9.18)

где 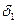, , 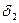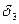- погрешности средств измерений, состав-ляющие измерительный канал.