Обработка результатов измерений

По ГОСТ 8.011-72 результаты измерения представ-ляют в следующем виде:

X = 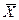± DX …, P,(9.1)

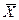где X - результат измерения; - среднее арифмети-ческое ряда наблюдений; 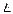X – основная погрешность измерения (граница доверительного интервала); Р – доверительная вероятность; … - единица измеряемой величины.

Оценку математического ожидания (среднего арифметического) 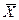находят по формуле

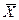= m_x = 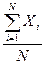, (9.2)

где X_i – результат i-го измерения; N – количество измере-ний.

Оценка среднего квадратического отклонения (СКО) 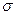характеризует степень рассеяния случайной величины около своего математического ожидания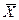

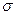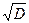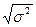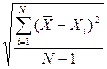= = = , (9.3)

где D – эмпирическая дисперсия (от лат. dispersio - рассеяние).

Доверительный интервал (от лат. intervalium - перерыв) – это статистическая оценка параметров вероятностного распределения, имеющего вид интервала, в котором с заданной вероятностью находится искомое значение параметра.

Эта вероятность называется доверительной вероят-ностью Р.

При ограниченном числе экспериментов (измерений) используют распределение Стьюдента (Student – псевдоним английского учёного начала ХХ века У. Госсета), которое по числу экспериментов (испытаний) N и доверительной вероятности Р позволяет найти коэффициент Стьюдента t_Ст, тогда

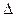Х = 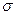× t_Ст. (9.4)

При неравноточных измерениях, когда результат измерения получен с помощью средств измерения, имеющих разную погрешность, имеем

р₁ : р₂ : р₃ = 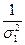: : 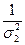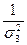, (9.5)

где 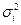- дисперсия измерения данного значения.

Тогда оценки математического ожидания результата измерения равна

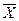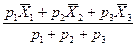= , (9.6)

а среднеквадратического отклонения

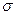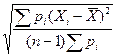= . (9.7)

Графической формой представления случайных чисел, сведённых в разряды, являются гистограмма (от греч. histos – здесь – столб и …грамма), т.е. столбчатая диаграмма, и полигон (поли… и греч. gonia - угол).

Последовательность построения гистограммы на оди-наковых разрядах следующая.

1. Находят наибольшее (X_max) и наименьшее (X_min) значения случайной величины и вычисляют размах изме-нения R

R = X_max - X_min. (9.8)

2. Задают некоторое число разрядов k. При n < 100 можно принять k = 6.

3. Определяют ширину разряда h = R/k. Для упрощения расчётов полученное значение h округляют в любую сторону.

4. Устанавливают границы разрядов и подсчитывают число измерений в каждом разряде. При подсчёте значения Х, находящегося на границе разряда, его следует всегда относить к разряду, расположенному слева или справа.

5. Устанавливают m_i - число значений Х, попавших в

данный разряд.

6. Определяют частоту появления величины p_i в данном разряде

p_i = 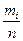, (9.9)

где n - общее число всех опытных данных.

7. В системе координат p_i = f(X) на ширине разряда h откладывают величину p_i как высоту и строят прямо-угольник.

Результат заносят в табл. 9.1.

Таблица 9.1