Характеристики надежности, определяемые с помощью моделей ТМО
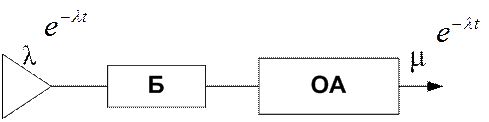
рис. 1
Если перейти к терминам теории надежности:
λ - интенсивность потока отказа (отказы, которые появляются в системе);
ОА - имитирует работу по восстановлению;
Основная сложность: формализовать работу ОА.
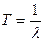 - время наработки на отказ;
- время наработки на отказ;
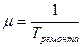
μ имитирует характеристики, показывающие сложность восстановления системы.
Если существует большое количество элементов (которые могут работать и отказывать), то образуется очередь на ремонт. В этом случае обслуживание ограниченное (ограниченное восстановление).
Характеристики надежности существенно разнятся при разных типах восстановления.
Тож - среднее время ожидания в очереди на обслуживание.
Тогда Твосст = Тобсл. заявки + Тож
Будем считать, что буфер (Б) неограничен, количество заявок неограниченно, обслуживание экспоненциальное, входной поток - пуассоновский.
Нарисуем для рис. 1 вероятностный граф. К формализации надо подходить разумно.
Факторы:
1) существенные и несущественные;
2) управляемые и неуправляемые.
ξ(t) - количество заявок в системе.
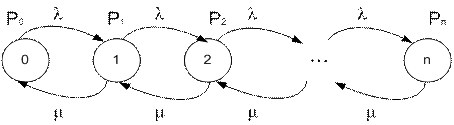
рис. 2
Этот граф называется цепочкой «гибели-размножения».
Будем считать, что система разомкнута (т.е. количество заявок неограниченно).
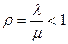 - загрузка.
- загрузка.
Рi - вероятность нахождения системы в i-м состоянии.
Р0 - вероятность того, что в любой момент времени застанем систему в
состоянии «0»
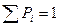
Зная вероятности, можно много чего найти:
1) среднее число заявок в системе:
1*Р1 + 2*Р2 + 3*Р3 + ...
τ = 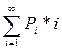
Если очередь большая, то ремонтные работы организованы плохо.
Пусть есть параллельная система (реальная):
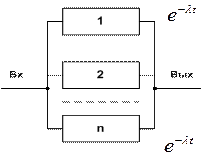
рис. 3
Будем считать, что система выходит из строя, когда выходит из строя последний элемент.
Эта система замкнутая, максимальное количество заявок равно n
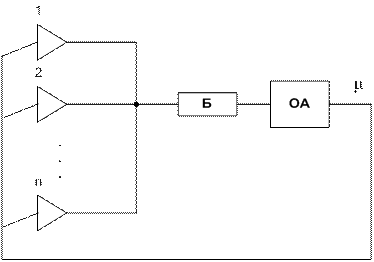
рис. 4
На рис. 4 изображена СМО, показывающая работу системы на рис. 3
Число состояний системы - n + 1
Вероятностный граф:
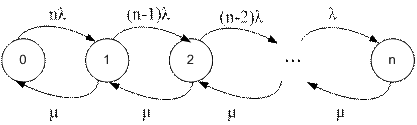
рис. 5
P0 = 1 - ρ
Состояние системы (ξ(t) )= количество заявок в системе.
Система, изображенная на рис. 3 - это композиция пуассоновских потоков.
Если восстановление неограниченно (т.е. нет очередей), то вероятностный граф будет иметь следующий вид (рис. 6):
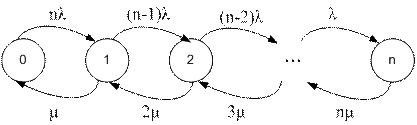
рис. 6
Т0 - время наработки на отказ - среднее время нахождения системы в группе
работоспособных состояний до 1-го выхода из этих состояний.
В общем случае вероятностный граф состояний имеет произвольный характер. Характеристики находятся следующим образом:
1) нарисовать вероятностный граф;
2) составить систему уравнений;
3) найти вероятности нахождения системы в каждом состоянии;
4) определить характеристики надежности;
а) Т0 - сред. время наработки на отказ;
б) Тр - сред. время ремонта системы;
в) Тож - сред. время ожидания ремонта;
г) τ - сред. длина очереди.
Тож = 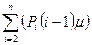
| <== предыдущая лекция | | | следующая лекция ==> |
| Система с параллельными соединениями. | | | Показатели надежности восстанавливаемых систем в процессе применения. |
Дата добавления: 2016-08-07; просмотров: 430;
